As estatísticas deste blog cumprem precisamente o princípio de Pareto: 20% dos posts geram 80% das visitas. Analisando esses 20%, destaca-se os posts dedicados a forma de calcular o tamanho de uma amostra representativa de uma pesquisa de opinião.
Observando o grande interesse por esta temática, hoje damos início a uma série de posts dedicados a amostragem: o que é, técnicas envolvidas,quando convêm usar uma ou outra, entre outros. Esperamos que os conteúdos sejam úteis para estudantes de pesquisa, pessoas curiosas e profissionais que desejam atualizar-se.

O que é "amostragem"?
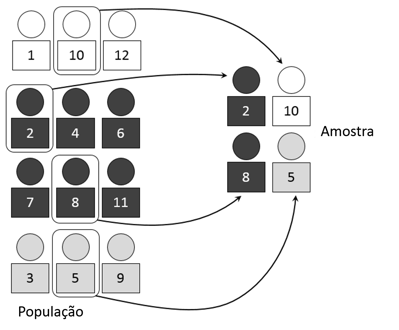
A amostragem é o processo de selecionar um grupo de indivíduos de uma população, a fim de estudar e caracterizar a população total.
A ideia é bastante simples. Imagine que você quer saber uma informação sobre um universo ou população, por exemplo, qual a porcentagem de fumantes no México. Uma maneira de obter essa informação é entrar em contato com todos os habitantes do México (122 milhões de pessoas) e perguntar se são fumantes. A outra maneira é selecionar um subconjunto de indivíduos (por exemplo, 1.000 pessoas) e perguntar se eles fumam.
O grupo de 1.000 pessoas formam uma amostra e a maneira como eu seleciono este grupo é chamado de amostragem.
No trecho anterior, introduzimos dois termos-chave nessa série de posts:
- Universo ou população: O número total de pessoas que desejam estudar ou caracterizar. No exemplo acima, é a população do México, mas podemos pensar em todos os tipos de universos, mais gerais e mais específicos. Por exemplo, se eu quero saber quantos cigarros os mexicanos fumam, o universo, neste caso, seria "fumantes de México".
- Amostra: O grupo de indivíduos do universo selecionados para o estudo, geralmente através de um questionário.
Por quê a amostragem funciona?
A amostragem é útil, pois permite acompanhar um processo inverso que chamamos de generalização. Para conhecer um universo, o que fazemos é: (1) Extrair uma amostra do mesmo, (2) Medir um dado ou opinião, (3) Projetar no universo o resultado observado na amostra. Esta projeção ou extrapolação recebe o nome de generalização dos resultados.
A generalização dos resultados pode apresentar algumas discrepâncias. Suponhamos que temos uma amostra aleatória de 1.000 pessoas, onde 25% da amostra fuma. A simples lógica nos diz que de 1.000 mexicanos entrevistados, 25% são fumantes. Se analisarmos 112 milhões de mexicanos, o número de fumantes deveria representar a mesma porcentagem de 25%. No entanto, deve-se tomar muito cuidado, pois através do acaso, poderíamos ter selecionados mais ou menos pessoas fumantes para representar a amostra. É muito comum encontrar resultados diferentes na amostra (25,2% de fumantes, por exemplo). Ou seja, a generalização dos resultados de uma amostra permite que o universo aceite alguns erros, conforme ilustra a figura abaixo:
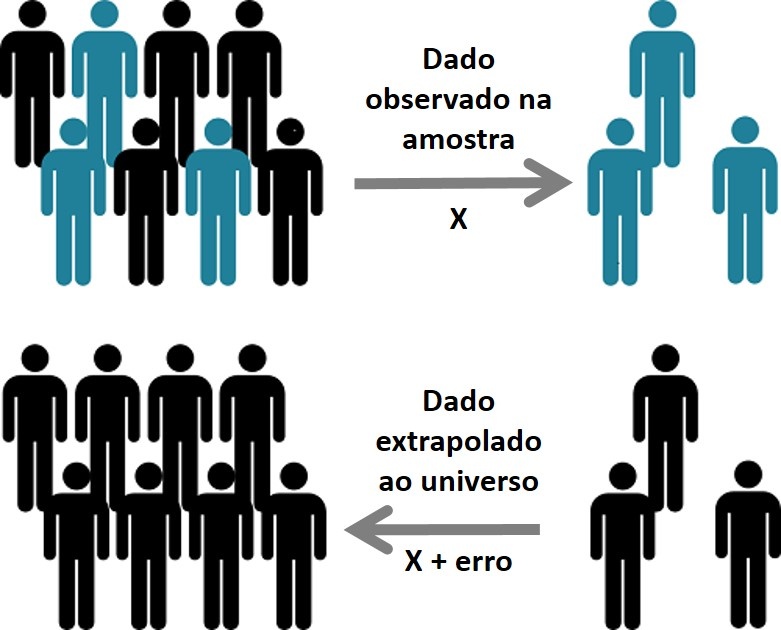
Felizmente, o erro cometido pela generalização de resultados pode ser limitado através de estatísticas. Para isso, usamos dois parâmetros: a margem de erro (diferença máxima entre os dados observados na minha amostra e os dados reais do universo) e o nível de confiança (nível de certeza sobre os dados reais que está dentro da margem de erro).
Por exemplo, no caso dos fumantes mexicanos, se selecionamos uma amostra de 471 indivíduos e perguntamos se eles fumam, o resultado obtido será uma margem de erro máxima de + 5% com um nível de confiança de 97%. Esta forma de expressar os resultados é correta quando se utiliza a amostragem.
O tamanho da amostra
Qual o tamanho da amostra que eu preciso para estudar um universo? Depende do tamanho do universo e do nível de erro que você está disposto a aceitar, como explicamos neste post. Quanto mais alta for a precisão, maior será a amostra necessária. Se você quiser ter absoluta certeza no resultado, até a última casa decimal, a amostra precisar ser tão grande quanto o universo.
Mas o tamanho da amostra tem uma propriedade fundamental que explica o porquê a amostragem utiliza diversas áreas do conhecimento. Esta propriedade pode ser resumida da seguinte forma: a medida que estudamos universos maiores, o tamanho da amostra cada vez mais representa uma porcentagem menor desse universo.
Este fenômeno é explicado de forma didática no website: Gaussianos.com, um blog interessante dedicado à matemática. Suponhamos que queremos fazer uma pesquisa para encontrar uma porcentagem (% de pessoas que fumam) com uma margem de erro de 5% e uma margem de confiança de 95%. Se o universo estudado englobar 100 pessoas, a amostra teria 79,5 indivíduos (ou seja, 79,5% do universo, que representa uma parte muito importante de todo o universo). Se o universo fosse de 1.000 pessoas, a minha amostra seria de 277,7 pessoas (27,7% do universo). E se o meu universo fosse 100.000, a amostra necessária seria de 382,7 pessoas (3,83% do universo).
Portanto, a medida que o universo for maior, a amostra deve crescer de forma desproporcional, com a tendência de estagnar, cada vez mais representando uma porcentagem menor do universo. Na verdade, a partir de um certo tamanho do universo (cerca de 100.000 indivíduos), o tamanho da amostra não cresce mais, conforme observamos no exemplo abaixo:
Tamanho da amostra necessária para obter nível de erro em 5% e nível de confiança em 95%
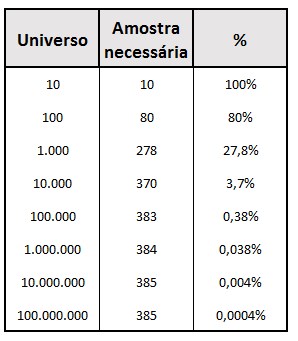
Os dados acima ilustram que não importa quão grande é o tamanho do universo, por exemplo, com 385 pessoas é possível estudar todos os dados com o mesmo nível de erro (margem de 5% e 95% de confiança). Por esta razão, a amostragem é tão poderosa: podemos afirmar dados altamente precisos de um grande número de indivíduos através de uma pequena parte do todo.
Em contrapartida, a amostragem não funciona muito bem em pequenos universos. Se eu tiver uma classe de 10 alunos, a opinião de cada um é fundamental para compreender a opinião global, não pode deixar de lado nenhum indivíduo. Para não apresentar falhas neste caso, é preciso considerar o universo de 10 indivíduos e examinar todos.
Vantagens e inconvenientes da amostragem:
Vantagens:
- Necessita estudar menos indivíduos e apresenta menos recursos (tempo e dinheiro);
- A manipulação de dados é muito mais simples. Se uma amostra de 1.000 pessoas é suficiente, para que eu preciso analisar um arquivo com milhões de registros?
Inconvenientes:
- Existe um erro controlado no resultado, devido a própria natureza da amostragem e a necessidade de generalizar os resultados;
Há um risco de má seleção da amostra. Por exemplo, se eu não selecionar os indivíduos de forma aleatória, meus resultados podem ser seriamente afetados.
A amostra aleatória simples: definição e alternativas
A teoria de amostragem baseia-se no conceito da amostra aleatória simples. É aquela amostra que seleciona indivíduos do universo de forma completamente aleatória. Sendo assim, todos os indivíduos devem ter a idêntica probabilidade (sem ser nula) de serem selecionados na amostra.
Um coisa é a teoria e a outra é a prática. Apenas em ambientes muito controlados é possível fazer com que as amostras sejam aleatórias. Além disso, quando temos universos compostos por grupos homogêneos (entre si) de pessoas, podemos aproveitar esse grupo para melhorar a qualidade da minha amostra (ou reduzir o tamanho dela).
- No próximo post iremos abordar quais tipos de amostragem existem, divididos por duas grandes famílias: a amostragem probabilística e a amostragem não probabilística. Esperamos por você!
ÍNDICE: Série "Amostragem"
- Amostragem: O que é e por quê funciona
- Amostragem probabilística e não probabilística
- Amostragem probabilística: Amostar aleatória simples
- Amostragem probabilística: Amostra estratificada
- Amostragem probabilística: Amostra sistemática
- Amostragem probabilística: Amostra por conglomerados
- Amostragem não probabilística: Amostra por conveniência
- Amostragem não probabilística: Amostra por quotas
- Amostragem não probabilística: Amostra por bola de neve