Si eres investigador de mercado y has obtenido muestras para tus estudios a través de un panel online, estarás familiarizado con el muestreo por cuotas. Si no es así, aquí tienes más información sobre esta técnica de muestreo.
Las cuotas son las proporciones que imponemos a una muestra (p.e. en cuanto a sexo, edad, región…) para que ésta se parezca a la población que queremos estudiar. Si fijamos más de una cuota en una muestra (p.e. sexo y edad), debemos escoger si aplicamos cuotas cruzadas o no cruzadas. Te explicábamos en este otro post el impacto de usar cada una de estas dos modalidades.
Si usamos cuotas no cruzadas, es frecuente que alguna cuota se complique, dificultando el cierre del trabajo de campo. Podemos acabar necesitando un perfil muy específico que a lo mejor es escaso en el panel (p.e. mujeres mayores de una región rural) para poder completar las cuotas correctamente.
Ante estas dificultades, es posible usar algo que se ha dado a conocer como soft quotas (cuotas blandas o flexibles). Hoy os explicamos qué son las soft quotas y analizamos hasta qué punto facilitan la obtención de muestras.

Recordatorio: cuotas no cruzadas
Antes de ver qué son las soft quotas, revisemos el concepto de cuotas no cruzadas. Imaginemos que queremos conseguir una muestra de N=600 personas a través de un panel online. Para que la muestra represente lo mejor posible la población, decidimos exigir unos objetivos (cuotas) para 3 variables diferentes:
- Región: queremos 120 participantes para cada una de las 5 regiones del país que estoy estudiando.
- Sexo: 300 participantes por cada uno de los 2 sexos.
- Edad: 200 participantes para cada uno de los 3 tramos de edad que he definido en mi proyecto (jóvenes, adultos, mayores).
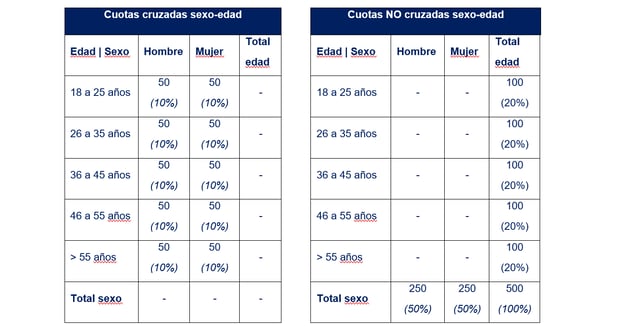
Estos objetivos los podemos representar con las siguientes tablas.
.
|
Cuota 1 |
N |
Cuota 2 |
N |
|
Cuota 3 |
N |
|
|
Región 1 |
120 |
Hombre |
300 |
Jóvenes |
200 |
||
|
Región 2 |
120 |
Mujer |
300 |
Adultos |
200 |
||
|
Región 3 |
120 |
|
Mayores |
200 |
|||
|
Región 4 |
120 |
|
|
|
|||
|
Región 5 |
120 |
|
|
|
Si exigimos el cumplimiento de estos objetivos por separado, estaremos hablando de cuotas no cruzadas. Eso significa que, mientras alcance mis objetivos por región, sexo y edad, no me preocuparé de la cantidad de encuestas que logre para cada combinación de estas variables. Las 150 persona de la región 1 podrían ser hombres, o todas las personas mayores podrían ser mujeres… Obviamente, no es lo que esperamos que suceda, pero no impondremos ningún control durante la recogida de datos para evitar estas situaciones. Por el contrario, unas cuotas cruzadas fijarían objetivos para cada combinación de región, sexo y edad: 20 respuestas para región1+hombre+joven, 20 para región1+hombre+adulto, etc.
El uso de cuotas no cruzadas puede encarecer los proyectos de forma notable, entre un +3% y un +200% respecto a la ausencia de cuotas, dependiendo de su complejidad.
Soft quotas
Las soft quotas son una forma de flexibilizar las cuotas no cruzadas, permitiendo cierta tolerancia respecto a los objetivos.
Por ejemplo, supongamos que aceptamos una tolerancia de ±10% respecto a los objetivos fijados. Eso significaría que, para la primera cuota del ejemplo, la de región, aceptaríamos como válido cualquier número de respuestas entre estos dos valores.
|
Cuota 1 |
Objetivo estricto |
Objetivo mínimo |
Objetivo máximo |
|
Región 1 |
120 |
≥108 |
≤132 |
|
Región 2 |
120 |
≥108 |
≤132 |
|
Región 3 |
120 |
≥108 |
≤132 |
|
Región 4 |
120 |
≥108 |
≤132 |
|
Región 5 |
120 |
≥108 |
≤132 |
Lo mismo haríamos con el resto de cuotas: la cuota de sexo admitiría un objetivo entre 270 y 330 respuestas para cada uno sus valores, y la de edad entre 180 y 220.
Una vez hemos obtenido las respuestas aceptando ciertas desviaciones, los datos deben analizarse corrigiendo estas pequeñas desviaciones, por ejemplo, usando ponderación. Esta corrección puede suponer la pérdida de precisión en las estimaciones, como te explicábamos en este post.
La cuestión es, ¿en qué medida flexibilizar objetivos hace el trabajo de campo más simple y económico? La respuesta es sorprendente.
Simulación de hard quotas
Para poder responder, hemos simulado una recogida de datos con muestro por cuotas usando R. En primer lugar, hemos simulado un muestreo sobre un panel online con cuotas cruzadas sin flexibilizar, es decir, usando hard quotas. En la simulación, hemos usado los siguientes supuestos:
- La probabilidad de participar de un individuo invitado en el panel es del 60%.
- La probabilidad de que participe a tiempo (dentro del periodo en el que aceptamos respuestas) es del 50%. Esto nos permite dar una estimación más real de los costes que produce una recolección de datos en un panel online, ya que es frecuente que muchos participantes traten de completar la encuesta fuera de plazo.
- Invitamos a un total de 3,000 panelistas a participar. Teniendo en cuenta los dos datos anteriores (probabilidad de participar y probabilidad de participar a tiempo), el número esperado de participaciones potencialmente válidas es 3,000 x 60% x 50% = 900, claramente superior a las 600 respuestas que necesitamos. Invitamos de más porque cuando fijamos cuotas en una muestra, siempre necesitamos más participantes de los que necesitaríamos si simplemente aceptásemos cualquier individuo como válido.
La forma en que simulamos la recolección de datos es simple:
1. A cada uno de los 3,000 invitados le asignamos una región, un sexo y una edad. Y lo hacemos proporcionalmente al objetivo de cuotas del estudio. Por lo tanto, las invitaciones guardan las mismas proporciones que las cuotas.
2. Para cada invitado, simulamos si participa y si lo hace a tiempo, de acuerdo a las probabilidades definidas anteriormente.
3. Cuando tenemos los invitados que participan a tiempo, los ordenamos aleatoriamente (para simular que pueden acceder a la encuesta en momentos diferentes) y vamos completando las cuotas de una en una.
4. Cuando completamos una cuota, por ejemplo, tenemos 300 mujeres, descartamos los siguientes participantes que forman parte de esa cuota.
Repetimos este proceso 1,000 veces y promediamos los resultados. Lo que obtenemos para un escenarios de cuotas estrictas es lo siguiente:
- El 67% de las simulaciones concluye con éxito: se obtienen las encuestas deseadas (600) respetando las cuotas estrictas.
- De media, es necesario descartar 300 participaciones que llegan dentro del tiempo establecido, pero que exceden las cuotas.
- De media, 900 participantes llegan fuera de plazo.
- Por lo tanto, 600/(600+300+900) es el % de participaciones válidas que obtenemos, un 33.3%. El resto, son participaciones descartadas.
Simulación de soft quotas
Supongamos ahora que usamos soft quotas y repetimos la simulación. Usar soft quotas implica algunas diferencias en la simulación.
1. No descartaremos participaciones salvo que excedan la cuota máxima, en lugar de la cuota estricta. Por ejemplo, si tenemos una tolerancia de ±10%, en lugar descartar a una mujer si ya tenemos 300 mujeres, lo haremos solo si ya tenemos 330 (un 10% más).
2. Respecto al mínimo de la cuota, no podemos hacer nada durante la recolección de los datos. Solo podemos esperar a tener el total de encuestas esperadas (600) y ver si hemos logrado los valores mínimos en todas las cuotas. De nuevo, si la tolerancia fuese ±10%, en lugar de exigir 300 mujeres, exigiremos 270 (un 10% menos).
Hemos hecho 1,000 simulaciones para 3 valores diferentes de tolerancia: ±1%, ±2.5%, ±5% y ±10%. Los resultados son los siguientes.
|
|
Hard quotas |
Soft quotas ±1% |
Soft quotas ±2.5% |
Soft quotas ±5% |
Soft quotas ±10% |
|
% éxito |
67% |
1% |
8% |
14% |
64% |
|
% logramos 600 encuestas |
67% |
94% |
99% |
100% |
100% |
|
% respetamos las cuotas |
67% |
0.8% |
8% |
14% |
64% |
El resultado es sorprendente. Resulta que flexibilizamos cuotas un 1%, y resulta casi imposible completar el proyecto con éxito: un 1% de las veces. Si aumentamos la tolerancia, mejoramos el % de casos en los que completamos el proyecto. Pero solo cuando alcanzamos una flexibilidad del ±10% logramos acercarnos al éxito obtenido sin flexibilizar: 64% vs 67%. Y, obviamente, a costa de desviarnos de las cuotas originales.
¿Por qué sucede esto? ¿Cómo puede ser que, flexibilizando cuotas, tengamos menos éxito? La clave para entender este fenómeno está en la diferencia entre las desviaciones positivas y negativas respecto a la cuota. Es decir, entre máximos y mínimos.
1. Al flexibilizar una cuota, fijamos un nuevo máximo que no permitimos superar. Durante la recolección de datos, descartamos aquellas participaciones que excedan este nuevo máximo. Por lo tanto, no vamos a superar nunca un máximo.
2. Sin embargo, no tenemos forma de asegurar que obtenemos el mínimo de respuestas de una cuota. Solo podemos recoger los datos, respetar los máximos y verificar al final si hemos cumplido con los mínimos.
Esta diferencia tiene un efecto global negativo. Porque las desviaciones positivas se reparten entre diferentes cuotas, pero las desviaciones negativas pueden acumularse sobre la misma cuota – por azar - sin que podamos hacer nada para evitarlo. De esta forma, cuando llegamos al máximo de 600 respuestas deseadas, nos encontramos que no hemos respetado las cuotas mínimas y el campo no se ha completado con éxito.
En las dos últimas filas de la tabla anterior, junto al % de éxito, hemos mostrado en qué % de casos hemos logrado 600 respuestas y en qué % hemos logrados que las cuotas estén entre el mínimo y el máximo. Observa que cuanto más flexibilizamos, es más simple lograr las 600 respuestas. Sin embargo, al flexibilizar, dificultamos mucho el cumplimiento de cuotas, es decir, la obtención del número de respuestas mínimas. Necesitamos flexibilizar mucho para obtener beneficios de las soft quotas.
Soft quotas asimétricas
Para resolver este problema, la solución es definir soft quotas asimétricas. Permitir mayor tolerancia en los mínimos que en los máximos. De esta forma, aunque varias desviaciones sobre máximos se produzcan a costa de la misma cuota mínima, es más difícil que la desviación supere el límite establecido.
Veamos esta técnica con un ejemplo. Tomemos como punto de partida el caso anterior con soft quotas simétricas de ±10%. Como hemos visto, estas cuotas daban un resultado ligeramente peor que las cuotas convencionales. Definir una cuota asimétrica es permitir una desviación positiva diferente a la negativa: por ejemplo, +10% y -5%. Esto se resume en el siguiente cuadro para la cuota sobre región.
|
Cuota 1 |
Objetivo estricta |
Objetivo mínimo -10% |
Objetivo máximo +5% |
|
Región 1 |
120 |
≥108 |
≤126 |
|
Región 2 |
120 |
≥108 |
≤126 |
|
Región 3 |
120 |
≥108 |
≤126 |
|
Región 4 |
120 |
≥108 |
≤126 |
|
Región 5 |
120 |
≥108 |
≤126 |
Para medir el efecto de la asimetría de cuotas, fijaremos una desviación de las cuotas mínimas de -10%, pero probaremos el efecto de limitar las cuotas máximas a +5%, +2.5% y +1%. Repitiendo el proceso de simulación anteriormente descrito, obtenemos:
|
|
Hard quotas |
Soft quotas ±10% |
Soft quotas +1%/-10% |
Soft quotas +2.5%/-10% |
Soft quotas +5%/-10% |
|
% éxito |
67% |
64% |
93% |
99% |
82% |
|
% logramos 600 encuestas |
67% |
100% |
100% |
100% |
82% |
|
% respetamos las cuotas |
67% |
64% |
93% |
99% |
100% |
La asimetría entre cuotas máximas y mínimas mejora drásticamente el % de casos en los que completamos con éxito la recolección de datos. En concreto, fijando un +2.5% de desviación positiva y -10% de desviación negativa, tenemos un éxito del 99%. Y eso se logra manteniendo el mismo número de encuestas válidas de los escenarios con hard quotas o con soft quotas simétricas ±10%: 33.3% de encuestas válidas del total de participaciones.
Ahorro de costes
El ejemplo anterior muestra que el uso de soft quotas asimétricas logra que, con un mismo número de invitaciones y participantes, podamos completar la recolección de datos con éxito en un mayor % de casos (99% respecto a 67%).
Podemos enfocar la cuestión al revés: para lograr el mismo % de éxito (99%) usando cuotas convencionales, necesitaríamos invitar a más personas, lograr más participantes y, por lo tanto, encarecer la recogida de datos. Pero, ¿en qué medida tendríamos que invitar más? ¿Cuánto encarecería la recogida de datos? O dicho de otra manera, ¿qué ahorro representa el uso de soft quotas asimétricas respecto a las cuotas no cruzadas estrictas?
De nuevo hemos recurrido a la simulación. Hemos incrementado la cantidad de personas invitadas a la encuesta manteniendo cuotas estrictas, hasta lograr un % de éxito del 99%, equivalente al éxito que obtenemos con las soft quotas asimétricas invitando a 3,000 personas.
El % de éxito que obtenemos a medida que invitamos más gente se muestra en la siguiente tabla.
|
Invitaciones |
% éxito |
|
3,000 |
67% |
|
3,600 |
94% |
|
3,700 |
95% |
|
3,800 |
96% |
|
3,900 |
98% |
|
4,000 |
99% |
La tabla anterior muestra que usando cuotas estrictas necesitamos invitar a 4,000 personas para obtener el mismo % de éxito que obtenemos con soft quotas asimétricas invitando a 3,000 personas (1,000 personas más, +33%). Invitar a más personas se traduce en más participaciones y más encuestas descartadas. En concreto, hemos pasado de tener un 33.3% de encuestas válidas a un 25.0% y, por lo tanto, hemos tenido que descartar 1,800 participantes en lugar de 1,250 (+600).
En términos de precio, esto supone aproximadamente un sobrecoste de +26%.
El desequilibrio ideal
Hemos visto que para una muestra de N=600 individuos con 3 cuotas de 5, 2 y 3 niveles, si admitimos una desviación negativa máxima de -10%, lo mejor es permitir una desviación positiva máxima de +2.5%, .una cuarta parte de la desviación negativa.
Esta proporción entre desviación positiva y negativa puede variar en función del tamaño de la muestra y del número de cuotas que apliquemos. Por ejemplo, manteniendo la configuración de cuotas anterior, hemos probado el efecto de la asimetría de cuotas para diferentes tamaños de muestra, que van de N=120 hasta N=1080, con incrementos de 120 individuos. El resultado se puede ver en el gráfico siguiente.
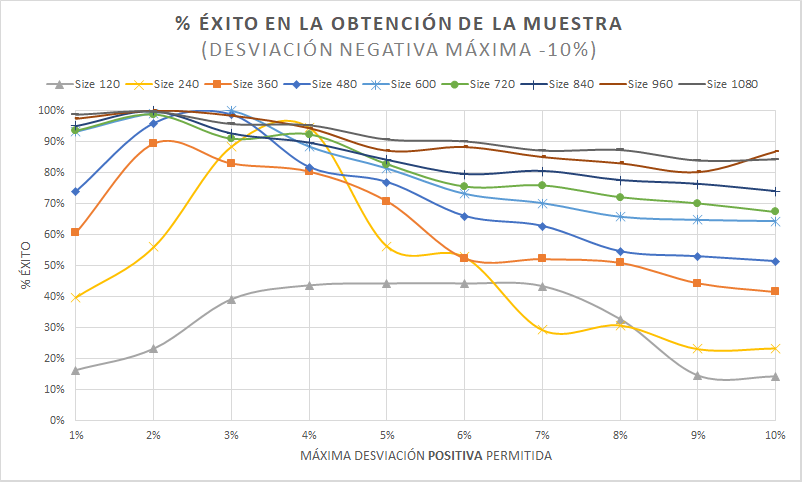
Observamos varias cosas en este gráfico:
1. A medida que tenemos un tamaño de muestra mayor, el % de éxito aumenta. Dicho de otra forma, dividir la muestra en cuotas hace más complicada la recogida de datos en muestras pequeñas. Es una cuestión estadística: es más fácil desviarse en términos relativos de un objetivo 60 hombres + 60 mujeres, que de un objetivo 540 hombres + 540 mujeres.
2. Fijando una desviación negativa de -10%, a medida que incrementamos la desviación positiva mejoramos el % de éxito, pero al seguir incrementando empeoramos. Por lo tanto, hay un óptimo en medio.
3. El óptimo tiende a reducirse a medida que aumentamos el tamaño de muestra. Para una muestra N=120 está en torno a +5%, para N=260 está en torno a +3.5%, para N=380 está 2%.... y con mayores incrementos tiende a estancarse entre 1% y 2%.
Conclusiones
El uso de soft quotas puede reducir significativamente el coste de las muestras que obtenemos de un panel online. Sin embargo, un mal uso de las mismas, puede ser contraproducente.
Para usar correctamente soft quotas debemos flexibilizar los objetivos de forma asimétrica: tolerar mayor desviación negativa que positiva. Al hacerlo, podemos reducir la cantidad de participantes necesarios y en consecuencia, el coste. El grado de asimetría debe ser mayor cuanto mayor es el tamaño de muestra.
Asimismo, en términos de representatividad, la asimetría de las soft quotas no empeora las proporciones de la muestra respecto a las soft quotas simétricas, al contrario: reduce las desviaciones positivas, manteniendo las negativas. Obviamente, en general, las soft quotas sí que empeoran la representatividad respecto a un muestreo por cuotas convencional.
Esperamos que este post te haya resultado de utilidad.