El Net Promoter Score (NPS) se ha convertido en una medida muy popular de satisfacción de clientes. Entre sus principales ventajas destacan la simplicidad, tanto para el cliente que opina como para el investigador que analiza los datos.
Sin embargo, pese a su popularidad, pocos investigadores acompañan los resultados de un estudio NPS con el correspondiente margen de error y nivel de confianza, como suele hacerse con otros resultados de encuestas. Esto impide valorar, por ejemplo, si una mejora del NPS del 5% es significativa o solo es una fluctuación aleatoria de los datos provocada por un tamaño de muestra reducido.
Hoy te explicamos cómo puedes hacerlo bien.
Lee también: ¿Qué es un NPS y cómo se mide?
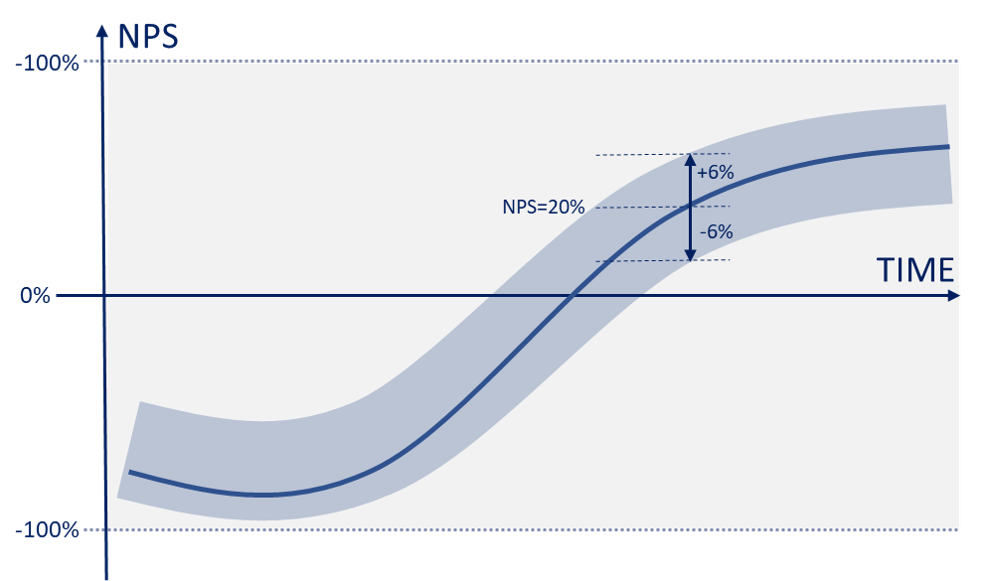
¿Cómo podemos calcular el margen de error?
El NPS se calcula sobre una muestra de n clientes y, como en todo muestreo, eso implica que podemos cometer cierto error de estimación respecto al NPS calculado sobre el total de la población de clientes.
Tal y como te hemos explicado en otros posts, para calcular el margen de error podemos recurrir al teorema central del límite. Según este teorema, la media de una variable aleatoria calculada en una muestra sigue una distribución Normal con media igual a la media poblacional y varianza igual a la varianza poblacional dividida por n.
Lee también: El muestreo: qué es y por qué funciona
Lo que puede confundir a muchos investigadores llegados a este punto es discernir cuál es la variable aleatoria. El NPS no es una variable aleatoria de los individuos de la población, sino que es el resultado de un cálculo entre proporciones de la muestra. Es decir, no se puede observar el NPS de un individuo aislado y por lo tanto, el NPS no es una variable aleatoria válida tal cual para aplicar el teorema central del límite.
La variable aleatoria que sí podemos observar de cada individuo es su opinión (op) respecto a nuestra compañía, que puede tomar 3 posibles valores: Promotores, Detractores y Neutros. Si codificamos esta variable asignando el valor -1 a los Detractores, el valor 0 a los Neutros y 1 a los Promotores, la media de esta variable es justamente el NPS:
$$ \text{NPS} = E[op] = \sum_{op=-1}^{1} op \cdot p(op) $$ $$ = (1) \cdot \frac{\#P}{n} + (0) \cdot \frac{\#N}{n} + (-1) \cdot \frac{\#D}{n} $$ $$ = \frac{\#P}{n} - \frac{\#D}{n} $$
Para calcular el margen de error nos falta la varianza de la variable op calculada en la población. La podemos aproximar con la varianza calculada sobre la muestra.
$$ \sigma^2 \approx \text{VAR}[op] = E\left[(op - E[op])^2\right] $$ $$ = (1 - \text{NPS})^2 \cdot \frac{\#P}{n} + (0 - \text{NPS})^2 \cdot \frac{\#N}{n} + (1 + \text{NPS})^2 \cdot \frac{\#D}{n} $$
Y por lo tanto, la desviación típica será la raíz cuadrada de la varianza.
$$ \sigma \approx \sqrt{ (1 - \text{NPS})^2 \cdot \frac{\#P}{n} + (0 - \text{NPS})^2 \cdot \frac{\#N}{n} + (1 + \text{NPS})^2 \cdot \frac{\#D}{n} } $$
Una vez tenemos la media y la desviación típica de la opinión de los clientes, podemos usar el teorema central del límite para calcular un margen de error. El NPS poblacional, el que nos interesa, se encuentra entre los límites siguientes:
$$ \text{NPS} \pm Z_{NC} \cdot \frac{\sigma}{\sqrt{n}} $$
donde NPS es la media de la opinión op en la muestra, σ la desviación típica de op, NC es el nivel de confianza con el que queremos hacer nuestra estimación, ZNC es el Z-score o valor crítico de corte de una distribución Normal para el nivel de confianza NC escogido y n es el tamaño de la muestra.
La cantidad ZNC ×σ/√n se conoce como margen de error. Recuerda: el valor ZNC depende del Nivel de Confianza que quieras usar para tu estimación. Los valores más habituales son los siguientes.
| Nivel de confianza NC | Z-score |
| 80% | 1.282 |
| 90% | 1.654 |
| 95% | 1.96 |
| 99% | 2.576 |
Ejemplo
Imagina que haces una encuesta a 500 personas, 200 de ellas resultan Promotores y 100 Detractores y, por lo tanto, 200 son Neutras.
El NPS resultante será
$$ \text{NPS} = \frac{\#P}{n} - \frac{\#D}{n} = \frac{200}{500} - \frac{100}{500} = 0.2 = 20\% $$
Para calcular el margen de error, calculamos primero la desviación de la variable opinión.
$$ \sigma \approx \sqrt{(1 - 0.2)^2 \frac{200}{500} + (0 - 0.2)^2 \frac{200}{500} + (1 + 0.2)^2 \frac{100}{500}} $$
$$ \sigma \approx \sqrt{0.8^2 \frac{200}{500} + 0.2^2 \frac{200}{500} + 1.2^2 \frac{100}{500}} = 0.75 = 75\% $$
Si queremos un Nivel de Confianza NC=90%, obtenemos que nuestra estimación del NPS es
$$ 20\% \pm 1.645 \frac{75\%}{\sqrt{500}} $$
$$ 20\% \pm 5.5\% $$
Si queremos un nivel de confianza más elevado, NC=95%, el margen de error aumenta:
$$ 20\% \pm 1.960 \frac{75\%}{\sqrt{500}} $$
$$ 20\% \pm 6.6\% $$
Tamaño de muestra
Ya sabemos cómo calcular el margen de error en un estudio NPS. Pero en ocasiones nos enfrentamos al problema inverso: tenemos que hacer el estudio y queremos asegurar de antemano que el margen de error no supera cierto límite e con un nivel de confianza NC.
En este caso, tenemos que invertir la fórmula anterior. Es decir, si queremos que
$$ Z_{NC} \frac{\sigma}{\sqrt{n}} \leq e $$
debemos usar una muestra de tamaño
$$ n \geq Z_{NC}^{2} \frac{\sigma^{2}}{e^{2}} $$
El problema en este caso es que no podemos estimar la desviación típica porque aún no tenemos datos acerca de cuántos Promotores, Detractores y Neutros hay en la muestra que obtendremos.
Pero podemos ponernos en el peor caso: la desviación máxima posible, que se produce cuando la dispersión en la población es máxima. Esto sucede si la mitad de la población son Promotores y la mitad Detractores. En ese caso, el valor NPS sería 0 y las proporciones de Promotores, Detractores y Neutros serían 1/2, 0 y 1/2 respectivamente. La desviación máxima resulta
$$ \sigma = \sqrt{(1 - 0)^{2} \cdot \frac{1}{2} + (0 - 0)^{2} \cdot 0 + (1 + 0)^{2} \cdot \frac{1}{2}} = 1 $$
Usando este resultado, el tamaño de muestra mínimo que necesitamos será
$$ n \geq \frac{Z_{NC}^{2}}{e^{2}} $$
Para los diferentes Niveles de Confianza habituales, tenemos
| Nivel de confianza NC | Tamaño de muestra |
| 80% | 1.64/e2 |
| 90% | 2.71/e2 |
| 95% | 3.84/e2 |
| 99% | 6.64/e2 |
Ejemplo
Supongamos que queremos hacer un estudio NPS y queremos que nuestras estimaciones no superen un margen de error del 5% con un nivel de confianza del 90%.
Tendremos que usar una muestra de
$$ n \geq \frac{2.71}{e^{2}} = \frac{2.71}{0.05^{2}} = 1084 $$
Ten en cuenta que este cálculo garantiza que el error no supera el 5% en el peor caso: aquel en el que una mitad de la población es promotora y la otra mitad es detractora. Si al realizar la encuesta no se produce este caso, el margen de error siempre será menor a este 5% y podrás calcularlo con las fórmulas que te hemos dado anteriormente.
Consideraciones finales
En los cálculos anteriores hemos aceptado la hipótesis de población infinita, hipótesis que suele aceptarse cuando la población es de al menos 100,000 individuos. Si consideras que la población la forman únicamente los clientes de tu compañía, posiblemente no llegues a un número tan elevado. Pero realmente puedes considerar como población a cualquier persona que potencialmente pueda contratar tus productos o servicios, por lo que siempre podrías acabar aceptando la hipótesis de población infinita. En cualquier caso, es posible hacer ajustes a las fórmulas cuando tu muestra representa una porción significativa del total de la población.
Lee también: ¿Qué tamaño de muestra necesito?
Por otra parte, en el cálculo del margen de error hemos aceptado que la desviación de la variable “opinión” en la muestra es una buena aproximación de la desviación en la población. Esto suele funcionar bien si tienes un número mínimo (5 o más suele ser suficiente) de observaciones de cada tipo (Promotores, Detractores y Neutros).
En definitiva…
Aplicar un poco de rigor estadístico a los estudios NPS es muy simple y evita malas interpretaciones. Es muy habitual encontrar casos en los que se hacen estudios NPS mensuales con apenas 20-30 respuestas, y en los que se afirman cosas como “este mes hemos mejorado el NPS en un 5%”. Con 30 respuestas, ¡el margen de error para un nivel de confianza del 90% es de ±25%! Un cambio del 5% puede significar muy poco.
Nuestro consejo es:
- Ten en cuenta el máximo error que estás dispuestos a aceptar antes de definir el tamaño de la muestra de un estudio NPS.
- Una vez hecho el estudio, acompaña los resultados con el margen de error y el nivel de confianza correspondiente.
----
En una versión anterior de este post cometí un error. Afirmaba que el máximo error muestral que podíamos observar en la población se daba "(...) cuando la dispersión en la población es máxima. Esto sucede si hay el mismo número de Promotores, Detractores y Neutros". Tal y como Jordi Bertrán (¡gracias!) me ha hecho observar, la desviación es mayor si la mitad de la población es promotora y la mitad detractora, dado que la variable con la que trabajamos es numérica y no categórica.
