Una de las técnicas de muestreo probabilístico más eficaces es el muestreo estratificado. Te lo explicábamos en uno de nuestros posts dedicados a técnicas de muestreo. Bien empleado, el muestreo estratificado ofrece mejores estimaciones que un muestreo aleatorio simple.
La versión no probabilística de esta técnica es el muestreo por cuotas. Y se basa en los mismos principios: dividir la población en subpoblaciones y obtener muestras de cada una de ellas.
Pero ¿por qué funciona esta técnica? Hoy te lo explicamos desde un punto de vista estadístico.
NOTA: Este post tiene fórmulas estadísticas, te recomendamos verlo en un laptop o, al menos, poniendo la pantalla de tu smartphone en posición horizontal.
Una población, dos subpoblaciones
El muestreo estratificado aprovecha la existencia de varias subpoblaciones dentro de una población. Mientras que el muestreo aleatorio simple considera la población como un todo, el muestreo estratificado obtiene muestras de tamaño prefijado para cada subpoblación.
Para ver las diferencias entre ambos métodos, veamos qué implicaciones tiene a nivel estadístico el hecho de que una población se componga de subpoblaciones. Vamos a verlo con un ejemplo simple: dos subpoblaciones.
Supongamos que queremos estimar la cantidad de calorías medias por día que ingiere una persona en Argentina. En este caso, podemos aceptar la habitual hipótesis de población infinita.
En este problema, es razonable pensar que hombres y mujeres consumen una cantidad diferente de calorías. Podemos considerar que son dos subpoblaciones.
Llamaremos x a la cantidad de calorías por día que consume una persona. Esta variable aleatoria x se distribuye de forma diferente para hombres y para mujeres. Llamemos fh(x) a la distribución de probabilidad de x en los hombres, y fm(x) en las mujeres. La distribución total de x es, por tanto
f(x) = pfh(x) + (1-p)fm(x)
donde p es la proporción de hombres en la población y 1-p la proporción de mujeres.
fh(x) y fm(x) pueden ser distribuciones diferentes, con diferentes medias (μh y μm) y desviaciones típicas (σh y σm). f(x) es el resultado de combinar ambas distribuciones, tal y como representamos a continuación.
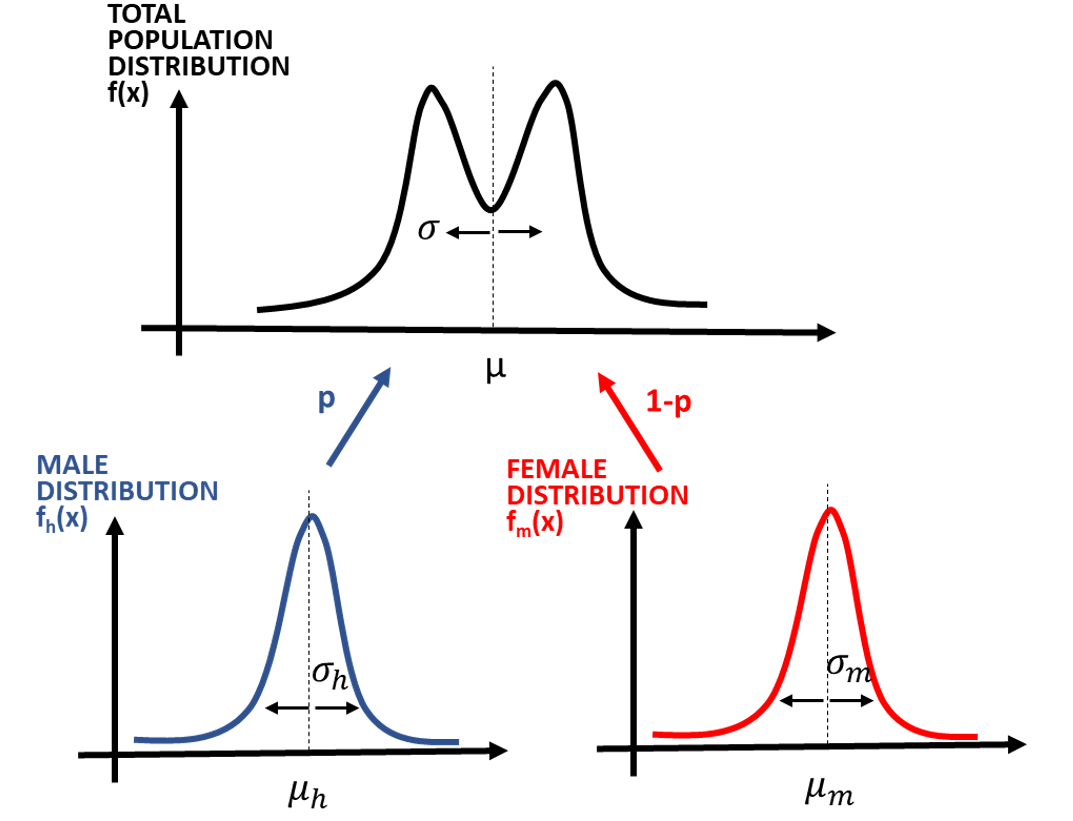
La población total tiene su propia media y desviación típica (o varianza), distintas de las de las subpoblaciones. Veamos qué relación tienen entre ellas. Empecemos con la media de la población. Como toda media de una variable aleatoria continua, se define como
E[x] = μ = ∞ ∫ -∞ xf(x)dx
En nuestro caso, dado que f(x) se compone de dos distribuciones, tenemos
μ = ∞ ∫ -∞ x(pfh(x) + (1-p)fm(x))dx
= p ∞ ∫ -∞ xfh(x)dx + (1-p) ∞ ∫ -∞ xfm(x)dx
= pμh + (1-p)μm
Tal y como esperábamos, la media poblacional es una media ponderada de las dos subpoblaciones.
La varianza de la población es más interesante. Recordemos primero cómo se calcula.
Var[x] = σ2 = E[(x - E[x])2] = E[x2] - E[x]2
El primer término (E[x2]) podemos desarrollarlo como sigue
E[x2] = ∞ ∫ -∞ x2(pfh(x) + (1-p)fm(x))dx
= p ∞ ∫ -∞ x2fh(x)dx + (1-p) ∞ ∫ -∞ x2fm(x)dx
= pE[xh2] + (1-p)E[xm2]
Usando la propia definición de varianza, pero en este caso en las subpoblaciones, sabemos que Var[xh]=E[xh2]- E[xh]2, y por tanto E[xh2]=Var[xh]+ E[xh]2=σh2 + μh2.Lo mismo aplica a xm. Reemplazando en la expresión anterior, tenemos
E[x2] = p(σh2 + μh2) +(1-p)(σm2 + μm2)
= pσh2 + pμh2 +(1-p)σm2 + (1-p)μm2
El segundo término (E[x]2) es simplemente el cuadrado de la media que ya habíamos calculado
E[x]2 = (pμh +(1-p)μm)2
= p2μh2 +(1-p)2μm2 + 2p(1-p)μhμm
Combinando ambos términos, tenemos
σ2 = E[x2] - E[x]2
=pσh2 + pμh2 +(1-p)σm2 + (1-p)μm2 - p2μh2 -(1-p)2μm2 - 2p(1-p)μhμm
=pσh2 +(1-p)σm2 + p(1-p)(μh2 + μm2 - 2μhμm)
=pσh2 +(1-p)σm2 + p(1-p)(μh - μm)2
Es decir, la varianza de una población compuesta de dos subpoblaciones tiene tres términos aditivos:
1. La varianza de la subpoblación de hombres, ponderada por su peso p en la población.
2. La varianza de la subpoblación de mujeres, ponderada por su peso 1-p en la población.
3. Un término proporcional al cuadrado de la diferencia entre medias de las dos subpoblaciones, multiplicado por el producto de las proporciones p(1-p).
Veamos ahora qué sucede cuando obtenemos una muestra de una población con estas características.
Muestreo sobre la población total
Ya lo vimos en un post anterior: obtenemos una muestra de la población y estimamos la media poblacional a través de la media de la muestra. Al hacer esto, el margen de error que asumimos depende de la varianza de la población dividida por n. En concreto
e = ZNC
σ √n
donde ZNC es un factor que depende del nivel de confianza que deseemos tener.
Si usamos muestreo aleatorio simple (MAS), estamos seleccionando n individuos directamente del total de la población. La varianza que afecta a nuestro margen de error es la varianza de la población total que acabamos de calcular. Por lo tanto, nuestro margen de error será
eMAS = ZNC
√ pσh2 +(1-p)σm2 + p(1-p)(μh - μm)2 √n
Muestreo sobre las subpoblaciones
Comparemos el resultado anterior con el que obtenemos al usar muestreo estratificado. En este caso, extraemos muestras independientes de tamaño prefijado de cada una de las subpoblaciones.
El tamaño de las muestras de cada subpoblación puede fijarse con diferentes criterios. Por el momento, usaremos el criterio más obvio: tamaño proporcional al peso que cada subpoblación tiene en la población. Siguiendo con nuestro ejemplo, obtendríamos una muestra de p×n hombres y una de (1-p)×n mujeres.
Al fijar los tamaños de las submuestras, eliminamos la posibilidad de que la muestra tenga una proporción de hombres y mujeres diferente a la de la población. En la práctica, esto equivale a (1) estimar la media de x en la muestra de hombres, (2) estimar la media de x en la muestra de mujeres y (3) estimar la media de x en la población como una combinación lineal de ambas estimaciones, ponderando por las proporciones reales de la población p y 1-p.
Este estimador tendrá por tanto la siguiente forma
x^ = pxh– + (1-p)xm–
La esperanza de esta estimación es la media poblacional que buscamos, tal y como sucedía con una muestra sobre el total de la población
E[x^] = E[pxh– + (1-p)xm–] = pμh + (1-p)μm
Pero las diferencias las encontramos en la varianza
Var[x^] = Var[pxh– + (1-p)xm–]
Para poder resolver esta expresión, usamos el hecho de que la varianza de una combinación lineal de variables aleatorias independientes cumple Var[aX+bY] = a2Var[X]+b2Var[Y]. Sabiendo esto
Var[x^] = p2Var[xh–] + (1-p)2Var[xm–]
La varianza total depende de la varianza de las estimaciones que hacemos mediante cada una de las muestras de las subpoblaciones (x−h y x−m). Estas varianzas muestrales, de acuerdo al teorema central del límite, son iguales a las varianzas de las subpoblaciones (σh2 y σm2) divididas por el tamaño de las respectivas muestras: p×n y (1-p)×n. Es decir
Var[x^] = p2
σh2 pn
+ (1-p)2
σm2 (1-p)n
=
pσh2 + (1-p)σm2 n
Por lo tanto, usando muestreo estratificado (EST) nuestro margen de error será
eEST = ZNC √Var[x^]
= ZNC
√ pσh2 +(1-p)σm2 √n
Diferencias entre ambos casos
Las diferencias que observamos al usar cada tipo de muestreo provienen de la varianza poblacional. Cuando obtenemos una muestra aleatoria del total de la población esta varianza es
pσh2 +(1-p)σm2 + p(1-p)(μh - μm)2
mientras que al obtener muestras de las subpoblaciones, la varianza resulta
pσh2 +(1-p)σm2
Por lo tanto, muestrear sobre el total de población cuando ésta se compone de dos subpoblaciones, produce un incremento de varianza que depende directamente de la diferencia entre las medias de las subpoblaciones.
+ p(1-p)(μh - μm)2
Este incremento afecta directamente a nuestro margen de error y hace que el beneficio de usar muestreo estratificado sea mayor...
1. ...cuanto mayor es la diferencia entre medias.
2. ...cuanto más equilibradas están las subpoblaciones (p=0.5), ya que el término p(1-p) es mayor.
Ejemplo con dos subpoblaciones
Volvamos a nuestro ejemplo inicial. La población argentina adulta, formada por aproximadamente un 50% de hombres y un 50% de mujeres. Queremos estimar el consumo medio de calorías diario mediante una encuesta a 500 personas. Es razonable pensar que hombres y mujeres forman subpoblaciones diferentes.
Supongamos que la población de hombres tiene una media de 2,200 calorías y una desviación típica de 100 calorías, mientras que las mujeres tienen una media de 1,950 calorías y una desviación de 75.
Tanto si empleamos muestreo aleatorio simple sobre el total de la población como muestreo estratificado, nuestra estimación del consumo medio que obtendremos estará centrado en torno al valor real (50%×2,200 + 50%×1,950=2,075).
Las diferencias las tenemos en el margen de error resultante al emplear cada método.
Supongamos que deseamos un nivel de confianza NC=90%. Empleando muestreo aleatorio simple (MAS), el margen de error es
eMAS = Z90%
√ 0.5×1002 +0.5×752 + 0.5×0.5(2,200 - 1,950)2 √500
= 1.645×6.85 = 11.26
Si empleamos muestreo estratificado (EST)
eEST = Z90%
√ 0.5×1002 +0.5×752 √500
= 1.645×3.95 = 6.50
El muestreo estratificado produce un margen de error un 42% menor al muestreo aleatorio simple. Esta reducción proviene de la diferencia entre medias de las poblaciones de hombres y mujeres.
Otras formas de mejorar las estimaciones
El muestreo estratificado que hemos estudiado en este post se conoce como proporcional, ya que el tamaño de las muestras es proporcional a su peso en la población. Es una elección obvia, pero no es necesariamente la mejor.
Recuperemos la expresión relativa a la varianza de la estimación usando muestreo estratificado
Var[x^] = p2
σh2 pn
+ (1-p)2
σm2 (1-p)n
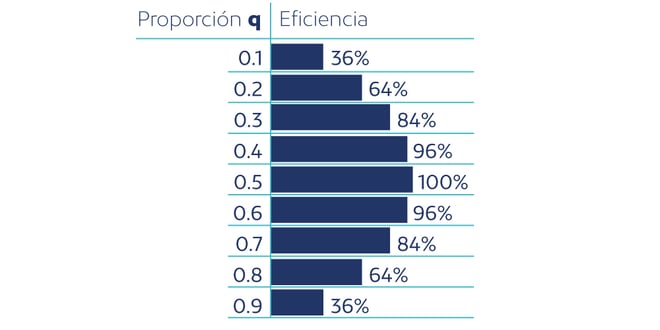
En este caso, p es la proporción de hombres en la población, y por tanto, la muestra de hombres tiene tamaño proporcional p×n. Pero supongamos por un momento que podemos fijar una proporción de hombres en la muestra q diferente de la proporción en la población p.
Var[x^] = p2
σh2 qn
+ (1-p)2
σm2 (1-q)n
=
1 n
(σh2
p2 q
+ σm2
(1-p)2 (1-q)
)Para reducir el error de estimación, nuestro objetivo es que la varianza de la estimación sea lo menor posible. Esta varianza no depende de las medias de las subpoblaciones, gracias a que usamos muestreo estratificado. Solo depende de (1) las varianzas de las subpoblaciones, (2) de la proporción poblacional p y (3) de la proporción muestral q.
Viendo esta fórmula, vemos que el muestreo proporcional que hemos empleado es la mejor opción si las varianzas de las subpoblaciones son iguales σh2=σm2=σs2 . Cuando esto sucede, la varianza es mínima si q=p, en cuyo caso
Var[x^] =
σs2 n
(
p2 q
+
(1-p)2 (1-q)
)=
σs2 n
( p + (1-p) ) =
σs2 n
Pero si las varianzas son diferentes, igualar las proporciones no es la mejor opción: es más eficiente dedicar más individuos de la muestra a la subpoblación más difícil de estimar, la que tiene mayor varianza. Esta técnica se conoce como muestreo estratificado de óptima varianza.
Para encontrar la proporción q óptima, tenemos que minimizar la siguiente expresión en relación a q:
( σh2
p2 q
+ σm2
(1-p)2 (1-q)
)Es un cálculo tedioso, pero sin ninguna dificultada matemática. Derivando la expresión anterior respecto a q e igualando a cero, encontramos que este valor es
qmin =
σhp σhp + σm(1-p)
La proporción óptima es la proporción poblacional ponderada por las desviaciones típicas de cada población. Este resultado aplica para cualquier número de subpoblaciones.
Ejemplo revisitado
En nuestro ejemplo anterior, las dos subpoblaciones de hombres y mujeres tienen diferente varianza: 1002 y 752 respectivamente. Podemos usar este hecho para ajustar el tamaño muestral de forma óptima.
Usando la fórmula anterior, resulta un valor qmin=0.57. Es decir, dado que la población de hombres tiene más variabilidad que la de mujeres, en lugar de emplear una muestra con 50% hombres, podemos usar un 57%.
Al usar estos tamaños muestrales, el margen de error resultante es
eEST = Z90% √ 1 n ( σh2 p2 q + σm2 (1-p)2 (1-q) )
= Z90% √ 1 500 ( 1002 0.52 0.57 + 752 0.52 0.43 )
= 1.645×3.91=6.44
Hemos reducido el margen de error de 6.50 a 6.44 (-1%). Es una ganancia muy limitada, ya que la diferencia en varianzas de las subpoblaciones es pequeña.
Conclusiones
El muestreo estratificado permite reducir el margen de error en estimaciones hechas sobre poblaciones formadas por dos o más subpoblaciones. Cuanto más dispares son las subpoblaciones, más beneficioso es el muestreo estratificado.
Si las subpoblaciones solo difieren en las medias, el muestreo estratificado proporcional es la opción más eficiente. Si, además, las subpoblaciones difieren en varianza, podemos emplear muestreo estratificado de óptima varianza. Sin embargo, esta técnica requiere saber de antemano las varianzas de las subpoblaciones o, al menos, qué proporción guardan entre ellas. Eso no es algo que habitualmente ocurra.
El muestreo por cuotas, pese a ser un método de muestreo no probabilístico, emplea el mismo principio. Si aceptamos que conocemos todas las posibles variables de segmentación que pueden influir en nuestra estimación, podemos definir subpoblaciones y obtener muestras de ellas. Sin embargo, no olvides nunca que no es formalmente correcto calcular un margen de error para una muestra no probabilística.
