Después de nuestra introducción a los análisis Conjoint, continuamos nuestra serie de posts dedicada a esta metodología hablando del concepto de utilidad, un concepto abstracto pero de enorme utilidad para describir el comportamiento del consumidor.
¿Qué es la utilidad?
En el anterior post vimos que un estudio Conjoint es capaz de calcular unos números que representan la utilidad que nuestros consumidores asignan a cada uno de los atributos que forman un producto. Pero, ¿qué es la utilidad y cómo debemos interpretarla?
La utilidad es un término usado en economía para describir el valor que recibe un consumidor de un bien (un producto, un servicio, una decisión cualquiera...). La utilidad puede medir cuanto disfruta alguien de una película, o la sensación de seguridad que obtiene al comprar un candado. Es posible considerar la utilidad de cualquier objeto o circunstancia, desde comerse una manzana hasta votar por un candidato en unas elecciones. Cualquier decisión que un individuo hace en su vida diaria puede verse como una comparación entre la utilidad que le proporciona esa decisión frente a otra. O frente a no tomar una decisión. En definitiva, el individuo elige aquellas elecciones que le proporcionan mayor utilidad.
Sólo las diferencias en utilidad importan
Podemos ir un poco más allá y cuantificar numéricamente la utilidad, de manera que no sólo podamos decir que una decisión es más útil que otra, sino cuanto más útil es. Eso es justamente lo que hace un análisis Conjoint. Estos números usados para medir utilidades sólo son válidos para hacer comparaciones.
Veamos algunos ejemplos que ilustran este principio. Afirmar que la utilidad que me proporciona el producto A es 100 no me da ninguna información. No significa nada en sí mismo. Utilidad=100 no tiene sentido al ser considerado de forma aislada.
Si la utilidad que me proporciona el producto A es 100 y la del producto B es 12.000, las utilidades empiezan a cobrar sentido. La comparación de ambas cantidades me informa de que B es más útil para mí que A, y que por lo tanto voy a elegir B. Sin embargo, no podría afirmar que B me proporciona 120 veces más utilidad que A, porque la utilidad no es una cantidad.
Del mismo modo, el signo de la utilidad puede ser positivo o negativo, no afecta a su interpretación. Si una opción A tiene una utilidad de -15 y una opción B de -10, seleccionaré la segunda por ser mayor que la primera. La mayor preferencia que tendré por B es idéntica a la que tendría si las utilidades fuesen 0 y 5 respectivamente: hay una diferencia de 5 en la utilidad en ambos casos.
La utilidad: racional pero subjetiva
En economía asumimos que el individuo se comporta de forma racional, y que por tanto siempre maximiza la utilidad en su toma de decisiones. Cada vez que un individuo elige, actúa racionalmente si elige la opción de mayor utilidad.
Sin embargo, la utilidad no es un concepto objetivo, sino que se define respecto a un individuo, teniendo en cuenta todas las circunstancias que lo rodean. La decisión de comer una chocolatina puede ser dañina para la salud de una persona, inconveniente si la comparamos con comer una pieza de fruta. Pero si el individuo, en el momento de tomar su decisión, ignora este daño o simplemente prioriza el disfrute que el chocolate le va a proporcionar en ese momento, estará percibiendo mayor utilidad de la chocolatina que de la fruta. El cálculo de utilidad tiene en cuenta todos los factores que conducen a una decisión determinada.
Relación entre utilidad y elección
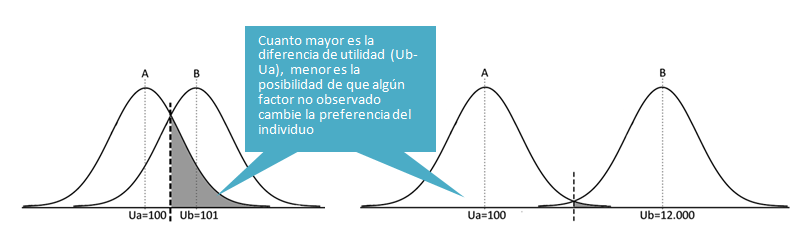
Un individuo siempre elige la opción que más utilidad le proporciona. Si A tiene una utilidad de 100 y B de 120, elegirá B. Y si A tiene una utilidad de 100 y B de 101, seguirá eligiendo B. Entonces, ¿qué importancia tiene la diferencia de utilidad? ¿Acaso sólo importa el hecho de que una opción tenga mayor o menor utilidad que otra?
Estrictamente es cierto: una vez conocemos la utilidad que percibe una persona de las diferentes opciones, sólo importa cuál es la de mayor utilidad. El individuo siempre elegirá esa opción, no importa lo cerca o lejos que estén las utilidades del resto de opciones.
El problema es que no podemos conocer a ciencia cierta la utilidad que percibe una persona. Sólo podemos tratar de medirla a través de diferentes métodos. El Conjoint es uno de esos métodos.
¿Por qué es importante la distinción entre conocer la utilidad y medirla? Porque toda medición conlleva un error. Supongamos que mido utilidades a través de un Conjoint, preguntando a un individuo sobre sus preferencias respecto a varias comparaciones de productos. Si el individuo se equivoca al responder una pregunta, estará introduciendo un error en mi medida de su utilidad. Asimismo, si cuando le describo los productos no he incluido los atributos que realmente afectan a su decisión, puede ser que su respuesta sea diferente a su decisión en circunstancias reales. Tanto una cosa como la otra – errores de respuesta y factores no observados – introducen cierto error de medida en la utilidad.
Estos errores de medida hacen que las diferencias de utilidades cobren importancia. Si la utilidad que he medido de A es 100 y la de B es 101, podría ser que los errores de medida estén desviando mi medición lo suficiente como para que en realidad la utilidad de B sea 99. Si eso pasa, mis mediciones me estarían diciendo que el individuo elegirá B pero en realidad elegirá A. Sin embargo, si la medida de A es 100 y la de B es 12.000, es mucho más difícil que los errores puedan hacer que en realidad la utilidad de B esté por debajo de A. Mi previsión de la elección del individuo es mucho más robusta.
Probabilidades de elección
Llegamos así a un concepto clave, el concepto de probabilidad de elección: es la probabilidad de que un individuo tome una decisión concreta, teniendo en cuenta la utilidad que he medido para cada opción y la posibilidad de que el error debido a factores no observados cambie esas utilidades.
Si determinamos que la opción A y la opción B tienen idéntica utilidad, diremos que la probabilidad de elección tanto de A como de B es del 50%. Si la utilidad de A es 10 y la utilidad de B es 11, diremos que la opción B tiene una probabilidad de elección mayor que la de A, pero sólo ligeramente, porque un pequeño error de medición podría hacer que A superase a B. Sin embargo, si la utilidad de A es 10 y la de B es 12.000, la probabilidad de elección de B se acercará al 100%.
Sólo nos queda resolver una cuestión. ¿Cómo determinamos la relación entre utilidad y probabilidad de elección? ¿Qué determina si la diferencia de utilidad de 1 unidad es grande o pequeña?
Modelo de comportamiento
La respuesta nos la facilita el modelo de comportamiento. Es el modelo estadístico que determina la relación entre las utilidades y las decisiones de los consumidores (es decir, las probabilidades de elección). Lo veremos con mayor detalle en posteriores posts, pero aquí os damos una visión general de esta cuestión.
Existen diferentes modelos de comportamiento. Unos son más simples y otros más complejos. Tendremos que elegir el mejor modelo para el problema que esté estudiando (y para las capacidades de análisis que tengo).
Veamos un ejemplo. El modelo de comportamiento más ampliamente usado en estudios Conjoint es el Logit Multinomial (MNL en adelante). Este modelo es muy popular por su simplicidad, gracias a algunas hipótesis que no siempre vamos a poder asumir. La principal es asumir que la utilidad es la misma para todo el mundo y que si los individuos eligen diferente, se debe a atributos no observados, que pueden ser diferentes para diferentes personas, y que generan error de medición. Según este modelo, si observásemos todos los atributos de los productos, ese error sería nulo y podríamos predecir perfectamente las decisiones de las personas.
Sabemos que en la práctica no es posible observar todos los factores, por lo tanto siempre tendremos error debido a factores no observados. MNL modela este error mediante una distribución de probabilidad conocida como distribución de valor extremo (extreme value). Es una distribución parecida a la normal o gaussiana: tiene mayor densidad en su zona central (el valor 0 es el más probable) y un rápido decaimiento a medida que nos alejamos del valor central. Pero a diferencia de la distribución normal, la distribución tipo valor extremo es integrable y nos permite conseguir una simple fórmula que relaciona utilidades y probabilidades de elección.
Para un caso con 3 opciones (A, B y C) para las que estimamos que la utilidad de cada opción es Ua, Ub y Uc, la probabilidad de que un individuo elija cada una de las opciones es.
Es posible extender esta fórmula para cualquier número de opciones. Y puedes comprobar fácilmente que la fórmula tiene muy buenas propiedades:
- Es fácil de calcular, las probabilidades siempre son positivas y suman 1.
- Si todas las opciones tienen la misma utilidad, las probabilidades de elección son idénticas.
- Si una opción tiene mayor utilidad que el resto, su probabilidad será más alta que la del resto. Y cuanto mayor sea la diferencia entre utilidades, mayor será su probabilidad de elección. Esto recoge la idea de que si la diferencia es muy grande, es más difícil que el error produzca un cambio en las elecciones.
¿Cómo nos ayuda esto en un estudio Conjoint?
La fórmula anterior predice qué opción elegirá un individuo si conocemos las utilidades de las opciones. Un estudio Conjoint trata de resolver el caso contrario: los individuos nos dicen qué opciones prefieren y nosotros calculamos las utilidades de las opciones.
Esta fórmula nos da la clave para el análisis, como veremos en posteriores posts. Debemos calcular las utilidades que predicen mejor las elecciones que hemos observado.
En el próximo post abordaremos, por fin, cómo llevar a cabo un estudio Conjoint. Qué fases comprende y qué opciones tenemos para cada una. Te esperamos.
¿Te ha gustado el post? ¿Quieres profundizar más sobre el tema? Pues hemos preparado una serie de diez cápsulas sobre Conjoint. ¡No te pierdas ninguna!
ÍNDICE: Serie Cápsulas sobre Conjoint
Cápsula 1: Qué es un estudio Conjoint y cómo utilizarlo
Cápsula 2: Entendiendo el concepto de utilidad
Cápsula 3: Fases de un Conjoint
Cápsula 4: Diseño experimental, parámetros de diseño
Cápsula 5: Diseño experimental, calidad de un diseño
Cápsula 6: Diseño experimental y estrategias para encontrar un buen diseño
Cápsula 7: Programación de cuestionarios Conjoint
Cápsula 8 - Análisis agregado de un Conjoint