Cuando investigamos a través de un panel online, siempre usamos muestreo por cuotas. Esta técnica produce muestras que tienen las mismas proporciones que la población que queremos estudiar, con relación a unas cuantas variables: por ejemplo, 50% hombres – 50% mujeres. Estas proporciones se conocen como cuotas.
Cuantas más cuotas fijamos en una muestra, más cara resulta. Hoy te explicamos por qué y te damos algunos consejos para no encarecer tu proyecto.
Sobre las cuotas
Fijar cuotas sobre una muestra es la forma en la que logramos que dicha muestra se parezca a la población, aunque el panel online no sea representativo en sí mismo.
Es posible fijar cuotas respecto a variables como sexo, edad, región, clase social… Por ejemplo, si en la población el 50% son hombres y el 50% son mujeres, puedo fijar una cuota de sexo en la muestra, de forma que forzamos esa misma proporción (50%-50%). Podemos fijar cuotas independientes para cada variable a controlar: 50% hombres y 50% mujeres, 80% de zonas urbanas y 20% de zonas rurales… O podemos ser más exigentes, y fijar un objetivo para cada combinación de las variables de interés: 40% hombres-urbanos, 40% mujeres-urbanas, 10% hombres-rurales… En el primer caso hablamos de cuotas no cruzadas, en el segundo de cuotas cruzadas.
El muestreo por cuotas no garantiza una representatividad perfecta. Pero si el problema que estamos investigando solo está afectado por las variables que usamos en las cuotas, la muestra debería ser útil.
Este hecho nos puede llevar a fijar un gran número de cuotas. Sin embargo, usar cuotas no es gratis: encarece la obtención de una muestra y puede llegar a hacerla inviable. Veamos por qué.
Un poco de nomenclatura
Antes de ir a los detalles, aclaremos la terminología.
Hablamos de una cuota para referirnos a la fijación de unos objetivos con relación a una variable. Por ejemplo, podemos hablar de una cuota de sexo.
Las cuotas fijan objetivos de respuesta para los diferentes tramos en que dividimos una variable. Si la variable es categórica (sexo) los tramos son las diferentes categorías (hombre y mujer) o agrupaciones de las mismas (provincias del norte, provincias del sur, …). Si la variable es numérica, es necesario definir tramos mediante intervalos (edad de 18 a 25 años, de 26 a 35…).
Cada objetivo asignado a un tramo se conoce como celda. Por ejemplo, una cuota de sexo define una celda para hombres y otra para mujeres. Si fijamos una cuota de edad, podemos definirla con 5 celdas: personas de 18 a 25 años, de 26 a 35, de 36 a 45, de 46 a 55 y mayores de 55.
Cuando fijamos dos o más cuotas en una misma muestra, podemos cruzar o no cruzar las cuotas. Si no las cruzamos, el objetivo de las celdas de cada cuota se controla por separado. Si las cruzamos, creamos nuevas celdas que son el resultado de combinar las celdas de cada una de las cuotas. El siguiente esquema muestra la diferencia para el ejemplo anterior (sexo y edad).
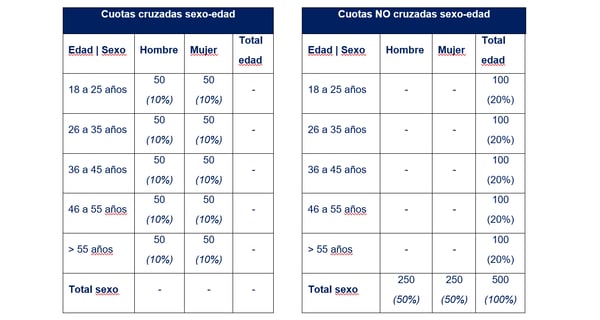
Observa que, en el caso de cuotas cruzadas (izquierda), tenemos objetivos para cada combinación de variables, un total de 2x5=10 celdas diferentes, cada una con un objetivo de 50 respuestas. Con cuotas no cruzadas, fijamos objetivos para cada variable por separado, y tenemos 2+5=7 celdas diferentes, 2 celdas con objetivo 250 y 5 celdas con objetivo 100.
Observa también que, en el escenario de cuotas cruzadas, cada celda es independiente: conseguir un hombre de 46 a 55 años no afecta al objetivo de mujeres de 46 a 55 años, o de hombres mayores de 55 años. En cambio, con cuotas no cruzadas, las celdas interactúan: cuando consigo una persona para la celda de “46 a 55 años”, necesariamente será hombre o mujer, y afecta a las celdas de “Hombres” o “Mujeres”.
Podemos resumir estas diferencias como sigue:
1. En general, usar cuotas cruzadas produce más celdas y es más exigente para el panel: es necesario tener participantes suficientes para cada combinación de variables. Típicamente, lograr mujeres mayores y hombre jóvenes en un panel online, es más difícil que otros perfiles.
2. Usar cuotas NO cruzadas, produce menos celdas (y eso es mejor). Y las celdas permiten jugar con la falta de disponibilidad de participantes en algunas combinaciones de variables. Por ejemplo, si me faltan hombres jóvenes, puedo suplirlos con hombre más mayores y mujeres jóvenes.
El coste de usar cuotas
Si las cuotas permiten que la muestra se parezca a la población, cuantas más cuotas mejor. Pero todo esto tiene un coste. Es una cuestión puramente estadística. Tal y como Ochoa y Porcar muestran en su paper “Modeling the effect of quota sampling on online fieldwork efficiency”, añadir cuotas equivale a dividir una muestra en submuestras de tamaño más pequeño. Conseguir respuestas suficientes para una muestra conlleva cierto riesgo, el riesgo de no lograr suficientes participantes. Este riesgo se mitiga enviando más invitaciones de las estrictamente necesarias.
Pues bien, si en lugar de tener una muestra tenemos varias submuestras, los riesgos se multiplican, obligando a enviar más y más invitaciones a participar. Eso produce inevitablemente que en algunas submuestras tengamos muchos más participantes de los que necesitamos. Esas participaciones, que en el argot del muestreo se llaman “quota-fulls”, deben descartarse, lo que supone un sobrecoste para los paneles.
Por lo tanto, cuanta mayor complejidad tenga una configuración de cuotas, más panelistas tenemos que descartar y mayor es el coste. Y más en concreto, cuantas más celdas definimos, más panelistas descartamos.
El siguiente gráfico muestra qué porcentaje de participaciones son válidas (lo que podemos llamar Eficiencia) en función de la cantidad de celdas en que dividimos la muestra (de 1 a 100), para diferentes tamaños de muestra (de 100 a 1000).
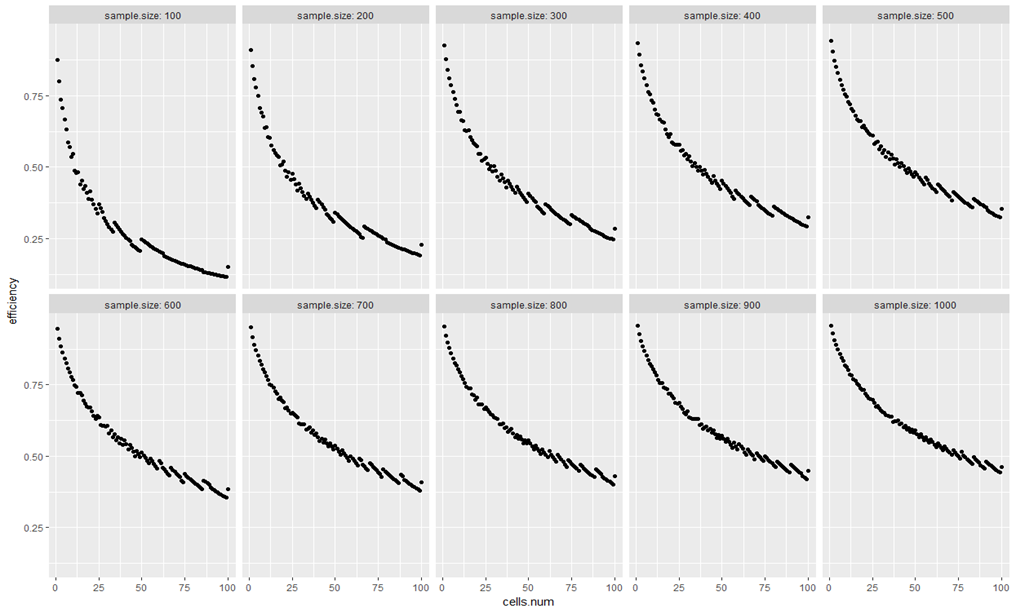 Para una muestra pequeña el impacto de dividir las encuestas en celdas es mayor que en una muestra grande. Por ejemplo, para una muestra de 100 individuos, pasar de 1 a 20 celdas reduce el % de encuestas válidas de 87.5% a 41.7%. Sin embargo, si la muestra es de 1000 individuos, pasamos de 95.8% a 73.1%.
Para una muestra pequeña el impacto de dividir las encuestas en celdas es mayor que en una muestra grande. Por ejemplo, para una muestra de 100 individuos, pasar de 1 a 20 celdas reduce el % de encuestas válidas de 87.5% a 41.7%. Sin embargo, si la muestra es de 1000 individuos, pasamos de 95.8% a 73.1%.
Ejemplos de sobrecoste, cuotas cruzadas
Ochoa y Porcar, 2017 facilitan ejemplos del sobrecoste que implica el uso cuotas. En la siguiente tabla puedes ver, para una muestra de 576 personas, cuantas respuestas debemos descartar para diferentes configuraciones de cuotas cruzadas. Por ejemplo, la primera fila indica que para 2 cuotas, cada una de 2 tramos (por ejemplo, sexo y dos tramos de edad), deberíamos descartar 94 personas para conseguir los 576 participantes válidos.
En la tabla se muestran casos con 3 y 4 cuotas, y con diferentes niveles por cada cuota. Y junto a cada escenario, hemos indicado una estimación del sobreprecio respecto a un escenario sin cuotas.
| Nº de cuotas | Tramos por cada cuota | Invitaciones necesarias* | Nº medio de participantes descartados | Descartados por cada encuesta válida | Sobreprecio estimado | |
| 2 | 2 | 2 | 2,232 | 94 | 0.16 | +3% | |
| 2 | 2 | 4 | 2,432 | 154 | 0.27 | +6% | |
| 2 | 2 | 8 | 2,752 | 250 | 0.43 | +20% | |
| 2 | 2 | 16 | 3,264 | 403 | 0.70 | +35% | |
| 2 | 2 | 32 | 4,160 | 672 | 1.17 | +50% | |
| 2 | 4 | 48 | 7,104 | 1,555 | 2.70 | +100% | |
| 2 | 2 | 288 | 15,552 | 4,090 | 7.10 | +200% | |
| 3 | 2 | 2 | 2 | 2,432 | 154 | 0.27 | +6% | |
| 3 | 2 | 2 | 3 | 2,592 | 202 | 0.35 | +20% | |
| 3 | 2 | 2 | 6 | 3,024 | 331 | 0.58 | +30% | |
| 3 | 2 | 4 | 8 | 4,160 | 672 | 1.17 | +50% | |
| 3 | 3 | 4 | 8 | 4,992 | 922 | 1.60 | +70% | |
| 3 | 3 | 4 | 48 | 15,552 | 4,090 | 7.10 | +200% | |
| 4 | 2 | 2 | 2 | 2 | 2,752 | 250 | 0.43 | +20% | |
| 4 | 2 | 2 | 2 | 4 | 3,264 | 403 | 0.70 | +35% | |
| 4 | 2 | 2 | 4 | 4 | 4,160 | 672 | 1.17 | +50% | |
| 4 | 2 | 2 | 4 | 6 | 4,992 | 922 | 1.60 | +70% | |
| 4 | 2 | 3 | 4 | 8 | 7,104 | 1,555 | 2.70 | +100% | |
| 4 | 2 | 3 | 8 | 12 | 15,552 | 4,090 | 7.10 | +200% | |
| * El número de invitaciones se calcula con una respuesta media de los participantes del 30%, con el objetivo de garantizar la consecución de las 576 encuestas completadas con un 95% de fiabilidad. | ||||||
Observa cómo a medida que aumentamos la complejidad de las cuotas, el número de encuestas descartadas aumenta. Para una configuración básica con 2 cuotas de 2 tramos, descartamos (de media) 94 personas. Si pasamos a 2 cuotas, una con 2 tramos y otra con 4, ya tenemos 154 descartados… Si vamos a configuraciones mínimamente complejas (3 cuotas, con 3, 4 y 8 tramos, algo relativamente habitual en investigación), tenemos 922 descartados. Es decir, hay más descartados que encuestas válidas.
El sobreprecio va de un 3% a un 200%, dependiendo de la complejidad.
Cuotas no cruzadas
Hemos comentado que usar cuotas no cruzadas produce menos celdas y permite más flexibilidad, compensando unos perfiles con otros. ¿Produce eso menos encuestas descartadas?
Ochoa y Porcar muestran en su estudio que no es así. Desde un punto de vista estadístico, las cuotas no cruzadas producen más encuestas descartadas. No es intuitivo, pero así es: la flexibilidad de las cuotas suele jugar en nuestra contra. Este fenómeno sucede cuando los participantes van ocupando las celdas de forma desequilibrada (por puro azar, o porque la tendencia a participar es diferente entre diferentes perfiles), llegando a una situación de bloqueo. Estos bloqueos se producen cuando dependemos de un perfil muy concreto, y ocasionalmente difícil, para cerrar el campo.
En los ejemplos teóricos mostrados por Ochoa y Porcar, usar cuotas no cruzadas puede reducir entre un 1% y un 16% la probabilidad de completar a tiempo un proyecto respecto a usar cuotas cruzadas.
Entonces, ¿Cuándo debemos usar cuotas no cruzadas?
La principal ventaja de las cuotas no cruzadas es poder obtener muestras que no serían factibles con cuotas cruzadas. En contra de lo que suele pensarse, las cuotas no cruzadas no son más económicas, pero sí que son las únicas posibles cuando hay escasez de determinados perfiles en un panel.
Esto sucede cuando una de las celdas cruzadas (por ejemplo, hombres jóvenes) puede suplirse con muestra de otras celdas (hombres mayores y mujeres jóvenes).
Algunos consejos
En vista de estos resultados, puedes seguir los siguientes consejos para obtener muestras fiables a un coste razonable:
1. Selecciona bien las variables: lo comentábamos en otro post, debes fijar cuotas sobre variables que (1) puedan afectar a tu estudio (por ejemplo, usamos sexo si hombres y mujeres tienen un consumo diferente de un producto) y/o (2) sean muy susceptibles de salir mal representadas en un panel online (por ejemplo, edad o clase social).
2. Prioriza tus cuotas y evalúa el coste de añadir las menos prioritarias. Posiblemente no puedas prescindir de sexo y edad, pero a lo mejor sí puedes prescindir de una cuota de región. Si no esperas grandes diferencias en el comportamiento por cuestiones geográficas, valora el coste que representa y el beneficio.
3. Si no hay un gran número de cuotas, mejor cuotas cruzadas, siempre y cuando el panel con el que trabajas pueda cubrir todas las celdas. Si el panel no puede, evalúa la opción de cuotas no cruzadas pero solicita el máximo esfuerzo para que no haya grandes desequilibrios (todos los hombre mayores, todas las mujeres jóvenes).
4. Si hay un gran número de cuotas y tramos por cuotas, seguramente es mejor usar cuotas no cruzadas ya que en caso contrario se disparará el número de celdas y el coste. De nuevo, asegúrate que el panel trata de hacer envíos compensados a todas las combinaciones de las variables de interés.
5. Si no puedes usar una cuota sobre una variable que es importante para ti (por coste, o porque el panel no tiene capacidad para asegurar el cumplimiento), solicita al menos envíos de invitaciones a participar bien repartidos.
6. Déjate aconsejar por expertos. Las empresas de panel online como Netquest recolectamos decenas de muestras diariamente y nos enfrentamos al problema de las cuotas a diario. Explícanos tu problema y te ayudaremos.
Esperamos que este post te haya servido de ayuda.
Referencias: “Modeling the effect of quota sampling on online fieldwork efficiency: An analysis of the connection between uncertainty and sample usage”, C Ochoa, JM Porcar, International Journal of Market Research, 2018.