En el último post vimos un método de análisis que nos permitía estimar utilidades para el conjunto de la muestra. Hoy veremos un método que nos permite calcular las utilidades de cada individuo. Es el modelo Jerárquico Bayesiano.
Limitaciones del modelo MNL
En el último post vimos el modelo MNL, capaz de estimar las utilidades de los atributos de un Conjoint a partir de las respuestas a las encuestas. Este modelo sólo permite analizar la muestra como un todo. Pero, ¿por qué no podemos usar este modelo persona por persona?
Técnicamente, nada nos impide usar el modelo MNL para analizar partes de la muestra o incluso individuos. Para hacerlo, simplemente tendríamos que analizar las respuestas de cada individuo por separado. En lugar de un análisis MNL haríamos tantos análisis como personas han participado en la encuesta.
Pero hacer algo así no es buena idea. El problema es que en un experimento Conjoint obtenemos muy poca información de cada persona, por lo que el análisis MNL nos daría resultados muy poco fiables, demasiado ajustados al caso concreto que ha visto cada individuo. Este problema, que en inglés se conoce como “overfitting”, se produce siempre que tratamos de generalizar conclusiones a partir de muy pocas observaciones. Para entendernos, sería como lanzar una moneda al aire, obtener 3 veces “cara” y afirmar a continuación que esa moneda tiene un 100% de probabilidades de arrojar “cara” como resultado.
Cantidad de información recogida
Durante un estudio Conjoint realizamos cientos de preguntas mostrando una gran variedad de comparaciones de productos. ¿Cómo es posible que un experimento así proporcione poca información?
Para responder, pensemos con detenimiento cuanta información obtenemos realmente. En un Conjoint típico con 5 atributos y 5 niveles por atributo, podemos generar 5x5x5x5x5 = 3.125 productos diferentes. Si preguntamos, por ejemplo, 10 preguntas a cada persona, cada una con 3 productos diferentes, como máximo un individuo va a ver 30 de los 3.125 productos posibles. No llega al 1%.
Si pensamos en el total de comparaciones de productos que podemos hacer, son un total de 9.762.500. En un cuestionario con 10 preguntas y 3 productos por pregunta, como máximo podemos hacer 30 comparaciones diferentes. Visto así, ya no parece tanta la información que observamos, ¿no?.
Estos números nos muestra una realidad: en un estudio Conjoint un individuo concreto ve muy pocos productos, a duras penas lograremos que vea unas pocas veces cada nivel de cada atributo, y es muy posible que algunas comparaciones de niveles no las vea nunca.
A este problema se añade otro: la cantidad de información que proporciona cada elección del respondiente. Cuando un individuo ve tres productos A, B y C, y nos dice que prefiere la opción C, nos informa de que la utilidad de C es mayor que la de A y la de B, pero no nos dice si es mucho mayor o sólo ligeramente. Tampoco nos dice si A>B o B>A. Dicho de otra manera, las elecciones entre productos contienen muy poca información.
¿Y qué podemos hacer?
El modelo MNL no es apropiado para analizar un individuo, pero sí para analizar un conjunto de individuos, gracias a los cuales obtenemos mucha más información. ¿Por qué no usamos la información del conjunto para completar la información que nos falta de cada individuo?
Esta idea es la que está detrás del algoritmo Jerárquico Bayesiano (Hierarchical Bayesian, HB). Este algoritmo combina información individual y agregada para mejorar la capacidad de estimación de cada persona. Siguiendo con la anterior metáfora de la moneda, sería algo así como lanzar una moneda 3 veces al aire, obtener 3 “caras" y, sabiendo que otras monedas como esa han arrojado un 50% de veces un resultado de “cara”, decir que esa moneda tiene una ligera tendencia (52%, por ejemplo) a arrojar más “caras” que “cruces”.
El modelo jerárquico
Veamos con un poco más de detalle cómo funciona el modelo HB. Se trata de un modelo con dos niveles, de ahí que se conozca como “jerárquico”:
- En el nivel más bajo, tenemos a los individuos. Cada individuo se comporta de acuerdo a un modelo MNL convencional independiente. Por lo tanto, cada persona asigna sus propias utilidades a los diferentes atributos, y su probabilidad de elección responde a la fórmula MNL.
- En el nivel más alto, las utilidades de cada atributo siguen una distribución de probabilidad concreta, generalmente una distribución normal multivariante. Por lo tanto, las utilidades de las diferentes personas de la muestra forman parte de esta distribución.
El doble nivel de este modelo permite resolver el problema de la falta de información individual. Al imponer que las utilidades de cada persona formen parte de una distribución de probabilidad conjunta, impedimos resultados disparatados a nivel individual. La visión conjunta obliga a que la utilidad individual se adecúe a una mirada global.
El enfoque bayesiano
Hemos visto porqué el modelo se denomina “jerárquico”. Veamos porqué también se llama “Bayesiano”.
En casi todos los métodos de análisis encontramos tres elementos comunes: los datos observados, el modelo que esperamos que nos ayude a explicar los datos y los parámetros que gobiernan el modelo. En un análisis convencional (no Bayesiano) lo que tratamos de obtener es la distribución de probabilidad de los datos dado el modelo y sus parámetros. Buscando los datos más probables encontramos los parámetros óptimos del modelo.
En un análisis Bayesiano damos la vuelta al problema: investigamos la distribución de probabilidad de los parámetros, dados los datos. Este tipo de modelos evitan tener que maximizar una función, sino que nos dan la probabilidad de cada posible valor de los parámetros. Otra virtud del enfoque Bayesiano: podemos incorporar al modelo información a priori que podamos tener, por ejemplo gracias a estudios anteriores.
Un modelo complejo
¿Cómo se analiza un modelo como el descrito anteriormente? Es mucho más complejo que un simple MNL. Piensa que ya no estamos buscando unas utilidades para cada nivel de cada atributo. Ahora debemos encontrar valores para:
- Las utilidades de cada nivel de cada atributo de cada individuo en la muestra.
- Las medias y varianzas-covarianzas de la distribución de probabilidad de las utilidades.
Por otra parte, nos enfrentamos a un problema mayor. A diferencia del modelo MNL, las expresiones matemáticas que describen la probabilidad de elección en el modelo HB no son cerradas, sino que contienen integrales que no tienen solución analítica. Para poder resolver el modelo, es necesario usar simulación.
La simulación es uno de los grandes avances en la resolución de modelos estadísticos avanzados. Se trata de un mecanismo que permite sortear un cálculo complejo mediante la extracción aleatoria de muestras de una distribución de probabilidad. Se basa en lo que se conoce como el muestreo de Gibbs.
De forma muy simplificada, podemos describir este método de la siguiente manera. Pretendemos obtener muestras de las utilidades que provengan de la distribución real. Para ello, la dificultad es que tenemos 3 grupos de parámetros: las utilidades, un vector de medias de la distribución de probabilidad que gobierna las utilidades y una matriz de varianzas-covarianzas de la misma distribución. El muestreo de Gibbs obtiene sucesivamente muestras de cada uno de estos 3 grupos de parámetros, fijando los dos restantes (condicionando sobre los dos restantes). Es posible demostrar que operando de esta forma, los parámetros convergen a los valores reales que buscamos.
Tiempo de cálculo
El proceso de simulación puede durar entre unos pocos minutos y varias horas, dependiendo de la complejidad del Conjoint. Habitualmente se itera un número de veces suficiente para garantizar que el algoritmo converge y, a partir de ese momento, se itera un número similar de veces para obtener valores válidos, los cuales promediamos para obtener resultados fiables.
Típicamente, la convergencia puede requerir 10.000 iteraciones y el periodo sobre el que se promedian los valores válidos suelen ser 10.000 iteraciones más.
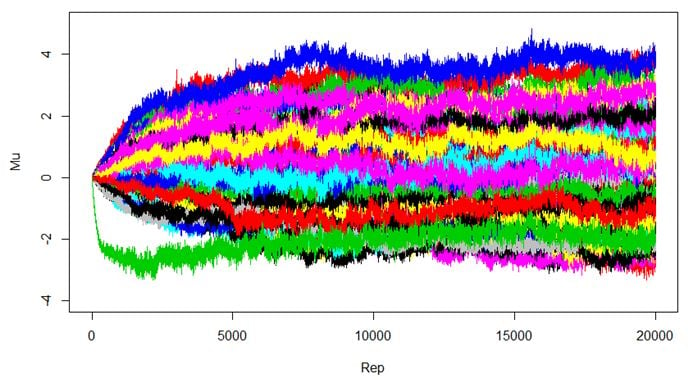
En la siguiente ilustración puedes ver cómo es el proceso. Inicialmente las utilidades se fijan a 0. En cuanto el algoritmo empieza su ejecución, las utilidades empiezan a desplazarse hasta que llegan a un punto en el que se estabilizan: ese punto es la convergencia. Promediando los valores a partir de ese punto tendríamos la estimación de utilidades que buscamos.
¿Qué hacer con las utilidades individuales?
Poder asignar un conjunto de utilidades a cada individuo en lugar de tener unas mismas utilidades para toda la muestra proporciona importantes ventajas:
- Podemos promediar utilidades por segmentos de población y ver si hay diferencias entre ellos (hombres vs mujeres, jóvenes vs mayores…)
- La predicción de elecciones futuras es más precisa. En lugar de predecir qué elegirá el conjunto de la muestra usando unas utilidades agregadas, podemos predecir la decisión de cada individuo y promediar dichas decisiones.
- Podemos buscar correlaciones entre utilidades y otras variables de los individuos.
En el próximo y último post desarrollaremos un caso real completo, desde el diseño hasta el análisis, para poder mostrar los contenidos explicados. Te esperamos.
¿Te ha gustado el post? ¿Quieres profundizar más sobre el tema? Pues hemos preparado una serie de diez cápsulas sobre Conjoint. ¡No te pierdas ninguna!
ÍNDICE: Serie Cápsulas sobre Conjoint
Cápsula 1: Qué es un estudio Conjoint y cómo utilizarlo
Cápsula 2: Entendiendo el concepto de utilidad
Cápsula 3: Fases de un Conjoint
Cápsula 4: Diseño experimental, parámetros de diseño
Cápsula 5: Diseño experimental, calidad de un diseño
Cápsula 6: Diseño experimental y estrategias para encontrar un buen diseño
Cápsula 7: Programación de cuestionarios Conjoint
Cápsula 8 - Análisis agregado de un Conjoint
Cápsula 9: Análisis Individual de un Conjoint