No último post, vimos um método de análise que permitiu estimar os ganhos para toda a amostra. Hoje vamos ver um método que nos permite calcular as utilidades de cada indivíduo. É o modelo hierárquico Bayesiano.
Limitações do modelo MNL
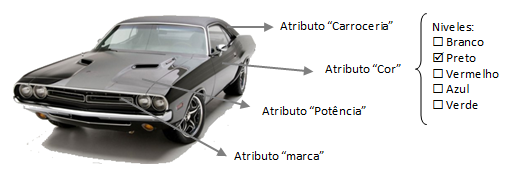
Na cápsula XIII, vimos que o modelo MNL é capaz de estimar as utilidades dos atributos de um Conjoint a partir das respostas da pesquisa. Este modelo só permite analisar a amostra como um todo. Mas, por que não podemos usar esse modelo individualmente?
Tecnicamente, nada nos impede de usar o modelo MNL para analisar partes da amostra ou mesmo indivíduos. Para isso, basta ter de analisar as respostas de cada indivíduo separadamente. Em vez de uma análise MNL, faríamos tanto análises como pessoas que participaram da pesquisa. Isso definitivamente não é uma boa ideia.
Num experimento Conjoint obtemos pouca informação sobre cada pessoa, de modo que a análise MNL daria resultados muito incertos, pouco concretos sobre cada indivíduo. Este problema, chamado de "overfitting" ocorre sempre que tentamos generalizar conclusões a partir de poucas observações. Seria como jogar uma moeda, obter "cara" 3 vezes e, em seguida, dizer que esta moeda tem 100% de chance ter "cara" como resultado.
Quantidade de informação
Durante um estudo Conjoint, realizamos mais de cem perguntas que mostram uma grande variedade de comparações de produtos. Como é possível um um experimento desses oferecer pouca informação?
Para responder a essa pergunta, considere cuidadosamente a quantidade de informação que realmente temos. Em um Conjoint típico com 5 atributos e 5 níveis por atributo, podemos gerar 5x5x5x5x5 = 3.125 produtos diferentes. Se perguntamos, por exemplo, 10 questões para cada pessoa, cada uma com três produtos diferentes, um indivíduo vai ver, no máximo, 30 de 3.125 produtos possíveis, ou seja, não chega a 1%.
Se pensarmos em comparações totais de produtos que podemos fazer, chegamos num total de 9.762.500. Em um questionário com 10 questões e 3 produtos por perguntas, no máximo, podemos fazer 30 diferentes comparações. Visto desta forma, já não parece tanta informação para observamos, certo?
Esses números nos mostram uma realidade: Num estudo Conjoint, um indivíduo específico vê poucos produtos, dificilmente vê alguns níveis de cada atributo, e é bem possível que algumas comparações de níveis nunca sejam vistas.
Esse problema leva à outro: a quantidade de informações fornecidas por cada escolha do entrevistado. Quando um indivíduo vê três produtos A, B e C, e diz que prefere a opção C, nos informa que o valor de C é maior do que A e B, mas não nos diz se ele é muito maior ou só ligeiramente. Também não sabemos dizer se A> B ou B> A. Em outras palavras, as escolhas entre os produtos contêm pouca informação.
E o que podemos fazer?
O modelo MNL não é adequado para a análise de um indivíduo, mas para analisar um conjunto de indivíduos, que podemos obter muito mais informações. Por que não usar as informações do conjunto para completar a informação que nos falta de cada indivíduo?
Esta é a ideia por trás do algoritmo hierárquico Bayesiano (Hierarchical Bayesian, HB). Este algoritmo combina a informação individual e a agregada para melhorar a capacidade de estimar cada pessoa. Seguindo a metáfora da moeda citada acima, seria algo como jogar uma moeda 3 vezes no ar, obter 3 "caras" e saber que em outras jogadas, 50% das vezes resultou em "cara". Dessa forma, pode-se dizer que essa moeda tem uma ligeira tendência (52%, por exemplo) de cair mais "cara" do que "coroa".
O modelo hierárquico
Vamos analisar como o modelo HB funciona. É um modelo com dois níveis, portanto, conhecido como "hierárquico":
- No nível mais baixo, temos os indivíduos. Cada indivíduo se comporta de acordo com um modelo convencional MNL independente. Portanto, cada pessoa atribui suas utilidades para os diferentes atributos e sua probabilidade de escolha corresponde a fórmula MNL.
- No nível mais alto, as utilidades de cada atributo segue uma distribuição de probabilidade particular, geralmente uma distribuição normal multivariada. Portanto, as utilidades das diferentes pessoas na amostra fazem parte desta distribuição.
O duplo nível deste modelo resolve o problema da falta de informação individual. Ao imponer que as utilidades de cada pessoa formem parte de uma distribuição de probabilidade conjunta, evitamos resultados discrepantes a nível individual. A visão conjunta obrigada que a utilidade individual se adapte a uma perspectiva global.
O modelo Bayesiano
Vimos por que o modelo é chamado de "hierárquico". Agora vamos ver por que também chamado de "Bayesiano".
Em quase todos os métodos de análise encontramos três elementos comuns: os dados observados, o modelo para nos ajudar a explicar os dados e parâmetros que regem o modelo. Em uma análise convencional, obtemos a distribuição de probabilidade dos dados, o modelo e seus parâmetros. Buscamos os dados mas prováveis e encontramos os parâmetros do modelo ideal.
Já em uma análise do modelo Bayesiano, voltamos para o problema: nós investigamos a distribuição da probabilidade dos parâmetros através dos dados fornecidos. Esse modelo evita ter que maximizar uma função, nos dá a probabilidade de cada possível valor de parâmetros. Outra virtude que o modelo Bayesiano oferece é a possibilidade de incorporar informações adicionais que possamos ter, por exemplo, resultados de estudos anteriores.
Um modelo complexo
Como se analisa o modelo Bayesiano? É muito mais complexo do que o MNL. Pense que já estamos bucando uutilidades para cada nível de cada atributo. Agora temos de encontrar valores para:
- As utilidades de cada nível, de cada atributo e de cada indivíduo na amostra.
- As médias e as variâncias-covariâncias da distribuição de probabilidades das utilidades.
Por outro lado, estamos diante de um grande problema. Ao contrário do modelo MNL, as expressões matemáticas que descrevem a probabilidade de escolha no modelo HB não estão fechadas mas contêm fatores que não têm solução analítica. Para resolver o modelo, é necessário utilizar uma simulação.
A simulação é um dos grandes avanços na resolução de modelos estatísticos avançados. Se trata de um mecanismo que permite desenhar um cálculo complexo por amostragem aleatória de uma distribuição de probabilidade. Ele é baseado no que é conhecido como amostragem Gibbs.
De uma maneira muito simplificada, vamos descrever este método. Temos a intenção de obter amostras das utilidades provenientes da distribuição real. Para fazer isso, a dificuldade é que temos 3 grupos de parâmetros: utilidades, um vetor das médias de distribuição de probabilidade que rege os utilitários e a matriz de variância-covariância da mesma distribuição. A amostragem Gibbs obtém sucessitivamente mostras de cada um dos 3 grupos de parâmetros, definindo os restantes . É possível demonstrar que, operando desta forma, os parâmetros convergem para os verdadeiros valores que buscamos.
Tempo de Cálculo
O processo de simulação pode durar de poucos minutos ou várias horas, dependendo da complexidade do Conjoint. Normalmente, se repete um número de vezes suficiente para assegurar que o algoritmo converge, e em seguida, a partir desse número, se recalcula um número similar de vezes para obter resultados confiáveis.
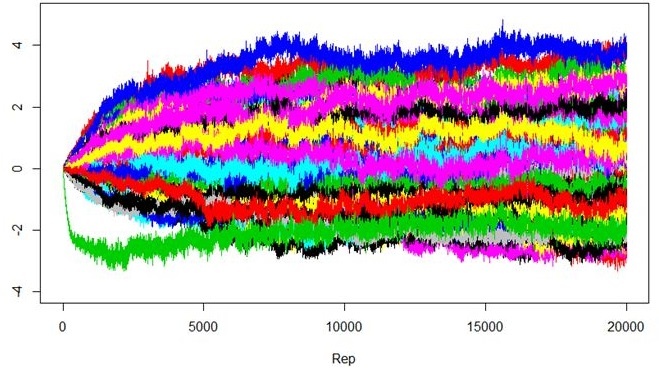
Normalmente, a convergência pode exigir 10.000 cálculos e para encontrar os valores válidos, mais 10.000 cálculos.Na ilustração abaixo você pode ver como funciona o processo. Inicialmente as utilidades são definidas em 0. Enquanto o algoritmo inicia a sua execução, os utilitários começam a se mover até que eles chegam a um ponto em que se estabilizam: este é o ponto de convergência. A média dos valores a partir desse ponto são as utilidades que buscamos.
O que fazer com as utilidades individuais?
Atribuir um conjunto de utilidades a cada indivíduo invés de uma única utilidade para toda a mostra pode proporcionar vantagens significativas:
- Podemos fazer uma média das utilidades por segmentos da população e verificar se existem diferenças entre eles (homens VS mulheres, jovens VS idosos, etc)
- A previsão de futuras escolhas é mais precisa. Em vez de prever o que elegirá o conjunto da mostra, podemos prever a escolha alguns indivíduos e definir a média das escolhas.
- Podemos buscar correlações entre as utilidades e outras variáveis dos indivíduos.
No próximo e último post sobre as Cápsulas Conjoint, iremos desenvolver um caso real completo, desde o desenho até a análise detalhada para poder ilustrar os conteúdos explicados.
Esperamos por você!