Continuando com a nossa série de posts dedicados a amostragem, hoje revisaremos a primeira de todas as técnicas de amostra probabilística: a amostragem aleatória simples. Esta técnica é uma das mais populares e serve como referência para todas as outras técnicas, mas como já discutimos anteriormente, na prática é difícil de ser usada.
Definição
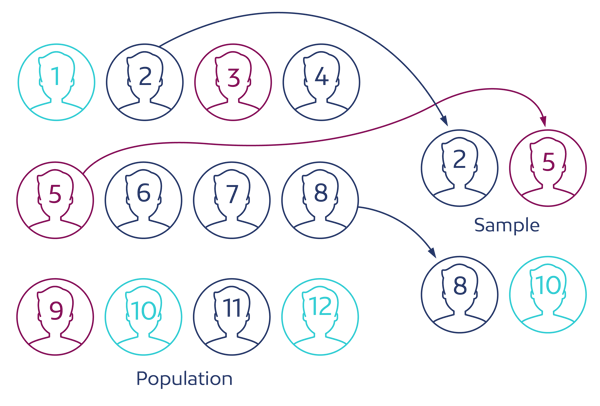
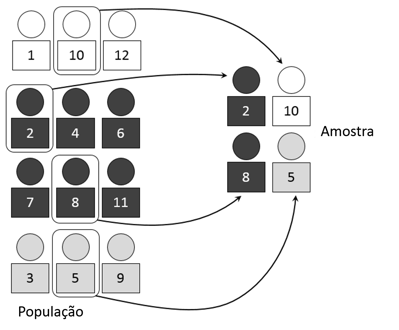
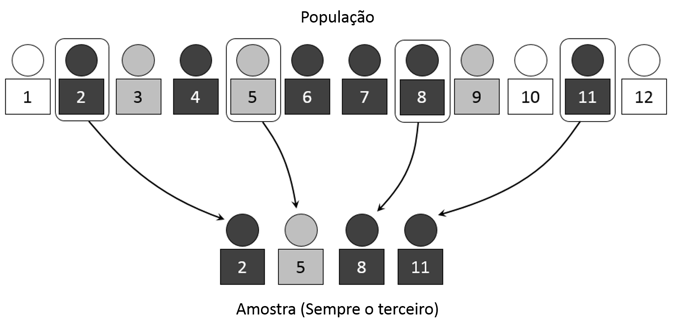
A amostragem aleatória simples (M.A.S.) é a técnica de amostragem onde todos os elementos que compõem o universo e estão descritos no marco amostral têm idêntica probabilidade de serem selecionados para a amostra. Seria como fazer um sorteio justo entre os indivíduos do universo: atribuir a cada pessoa um bilhete com um número de série, introduzir os números em uma caixa e sortear um número aleatório. Todos os indivíduos têm este bilhete dentro da urna formam uma amostra. Obviamente, na prática, estes métodos podem ser automatizados usando computadores
Se os indivíduos de um universo podem ser selecionados mais de uma vez na amostra, estamos falando de M.A.S. com repetição ou sem repetição. Se usamos a repetição, se eu seleciono um indivíduo aleatoriamente num sorteio, isso não me impede de selecioná-lo novamente num seguinte sorteio. Seria equivalente a dizer que toda vez que eu vou sortear um número aleatório de minha urna, eu adiciono novamente este número para participar do próximo sorteio. Se, no entanto, nós não usamos a repetição, um indivíduo selecionado para a amostra só poderá ser selecionado uma única vez.
A pergunta óbvia é "o que é melhor, usar a reposição ou não?" É um simples problema matemático. César Pérez López, em seu livro "Amostragem Estatística" (Pearson, 2005) desenvolve uma forma muito clara de comparação entre ambas as técnicas. Podemos olhar para o ponto de vista que a técnica gera estimativas mais precisas e do ponto de vista que a técnica permite ter a mesma precisão se eu utilizo uma amostra menor. Concluiu-se que a amostragem aleatória simples sem reposição sempre é mais eficiente.
Para poder observar este resultado, temos a seguinte expressão que define o tamanho das amostras em M.A.S. sem reposição. A fórmula relaciona o tamanho da amostra necessária quando o universo é finito com o tamanho da amostra quando o universo é infinito:
onde n0 é o tamanho da amostra necessária para um universo infinito e N é o tamanho do universo finito. É possível demonstrar que o tamanho da amostra quando usamos repetição (nr) é sempre igual ao tamanho necessário para universo infinito (nr=n0). Se isso ocorrer, podemos afirmar que:
Portanto, o tamanho da amostra utilizada quando não usamos reposição é sempre menor do que o exigido se usamos reposição. Este resultado coincide com a intuição: se estamos utilizando a reposição e, por acaso, selecionamos um indivíduo mais de uma vez na mesma amostra, o efeito é semelhante ao da redução do tamanho da amostra, onde observa-se uma menor diversidade de indivíduos. Da mesma forma, se o universo é infinito, ambos os métodos coincidem, uma vez que a probabilidade de eu selecionar o mesmo indivíduo duas vezes na mesma amostra tende a ser infinitamente pequena.
✔ Benefícios da amostra aleatória simples
Com o desenvolvimento da informática, é possível desenhar uma amostra aleatória simples de forma rápida e totalmente confiável. A geração de números aleatórios mediante a softwares (são números estritamente pseudo-aleatórios) é cada vez mais confiável.
Desta forma, ao utilizar M.A.S., nos asseguramos a obtenção de amostras representativas de modo que a única fonte de erro que poderá afetar meus resultados será o azar aleatório. Importante: este "erro" devido ao azar pode ser calculado com precisão. Iremos aprender este conteúdo no próximo post!
✘ Inconvenientes da amostra aleatória simples
O único inconveniente da M.A.S. é a dificuldade de aplicar nas pesquisas reais. Vamos recordar: por ser uma técnica probabilística, é necessário um marco amostral considerando todos os indivíduos onde todos sejam selecionáveis para a minha amostra. Um requisito dificílimo para ser cumprido, pois na maioria dos estudos de mercado e opiniões reais que nos obrigam a aplicar outras técnicas.
No próximo post iremos estudar outra técnica de amostra probabilística muito popular: a amostragem estratificada. Esperamos por você!
ÍNDICE: Série "Amostragem"
- Amostragem: O que é e por quê funciona
- Amostragem probabilística e não probabilística
- Amostragem probabilística: Amostar aleatória simples
- Amostragem probabilística: Amostra estratificada
- Amostragem probabilística: Amostra sistemática
- Amostragem probabilística: Amostra por conglomerados
- Amostragem não probabilística: Amostra por conveniência
- Amostragem não probabilística: Amostra por quotas
- Amostragem não probabilística: Amostra por bola de neve