Hoy quiero contaros algo sobre una curiosidad estadística que puede ser muy útil a cualquier persona que tenga que hacer una predicción cuantitativa. La situación típica podría ser la siguiente: supongamos que queremos estimar las ventas que tendremos en la empresa este mes, concretamente, el número de unidades que se habrán vendido entre el día 1 y el 31 del mes. Y supongamos que para hacer esta estimación contamos únicamente con 2 expertos, por un lado, un compañero del departamento financiero especializado en controlling financiero, que dice que serán 100 unidades. Por otro lado, un segundo experto, en este caso un estadístico externo especializado, que concluye que venderemos 200. No hay más datos. ¿Qué hacer? ¿A quién creer? ¿Al controller interno o al estadístico externo? Supongamos que la realidad finalmente resulta ser X (no la desvelaremos de momento). Es fácil calcular el error de la predicción: si habíamos escogido 100, el error de predicción será el valor absoluto de la resta 100-X. En caso de haber escogido 200, la diferencia o error habrá sido el valor absoluto de 200-X. Claro…el problema es que no conocemos X, así que no parece posible saber a ciencia cierta cuál de los expertos es mejor. De hecho, ¿tenemos información a priori sobre quién podría ser mejor? En realidad parece que no. Podemos creer que tenemos razones para escoger (apuesto a que más de un lector tiene a estas alturas ya una “apuesta personal” sobre qué experto es mejor a priori), pero lo cierto es que no tenemos ningún dato en este problema que nos permita decantarnos por ninguno; ¡creer lo contrario es un defecto de serie que tenemos los humanos!
Veamos las consecuencias de este “defecto humano”. Como no hay razones sólidas para escoger uno u otro, podemos suponer que la mitad de las personas escogerán uno y la otra mitad el otro. Por lo tanto, el error medio que cometemos si escogemos uno de los expertos al azar será: Error1 = 0,5x[100-X]+0,5x[200-X]=([100-X]+[200-X])/2. (utilizo los corchetes para indicar “valor absoluto”).
Y aquí es donde quería llegar. La pregunta obvia es: ¿se puede mejorar este error esperado? A primera vista parece que no, pero conviene detenerse a analizarlo. De hecho, la primera estrategia alternativa en la que todos pensamos cuando estamos en situaciones parecidas es utilizar el promedio entre las dos predicciones, en este caso: (100+200)/2. La intuición que tenemos sin embargo es que el error esperado de predicción de este promedio es el mismo que el que tendríamos escogiendo un experto al azar como en el párrafo anterior. Pero…¿es así? Calculémoslo: Error2=[(100+200)/2-X]=[(100+200)/2-2X/2] =([100-X+200-X])/2.
Para comparar parece claro que queremos ver cuál de los errores esperados es menor. Así que básicamente debemos comparar [100-X]+[200-X] con [100-X+200-X]. No hay duda de que lo segundo es siempre (!) menor o igual a lo primero, cualquiera que sea el valor de X. En realidad, podéis comprobar que siempre que X caiga entre 100 y 200, entonces Error2<Error1; y cuando X se sitúe fuera del intervalo de las dos predicciones, entonces Error2=Error1. Por lo tanto, en un problema de esta naturaleza, ¡utilizar la media de las predicciones es siempre beneficioso!
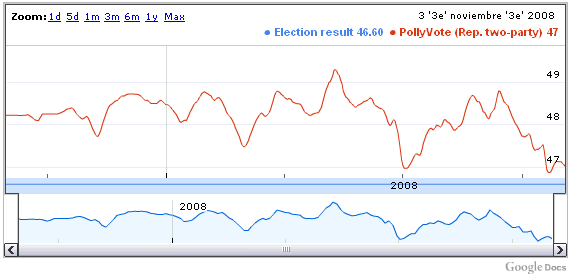
Al principio que acabo de exponer hay quien le llama ‘averaging principle’, y es conocido al menos desde Kelley,1925. Pero es muy contraintuitivo para quien lo piensa por primera vez. Eso explica las fuertes reticencias que tienen muchos investigadores a la hora de combinar metodologías, pese a que en realidad promediar resultados de estudios que han utilizado diferentes metodologías seguramente es muy beneficioso. Claro, promediar es mejor salvo cuando el investigador tiene fuertes indicios de que uno de los estimadores individuales es un mejor “experto”…En general, sin embargo, es mucho más rentable ser humildes, combinar y promediar. Eso es lo que hace por ejemplo ww.pollyvote.com, que logró pronosticar con mucha precisión el resultado de las pasadas elecciones en EEUU combinando 4 fuentes de datos con metodologías completamente diferentes; y lo hizo aplicando ni más ni menos que el ‘averaging principle’.
Las cuatro fuentes de pollyvote fueron:
1. Resultados combinados y corregidos de sondeos electorales
2. Previsiones de un panel de expertos en política norteamericana
3. Mercado Electrónico de Predicciones de IOWA
4. Modelos Cuantitativos