¿Tiene mi encuesta una diferencia significativa?

En un post anterior tratábamos de explicar cómo debo decidir el tamaño de una muestra para garantizar que los datos que obtengo van a estar dentro de un margen de error controlado. Hoy vamos a tratar un tema relacionado: cuando observo una diferencia en un dato de una encuesta, ¿es esa diferencia estadísticamente significativa?

¿Es real o es azar?

Es una pregunta que nos formulamos a menudo, incluso en situaciones de nuestra vida cotidiana. Supongamos que normalmente voy a mi lugar de trabajo en coche por una ruta A y tardo, en promedio, 25 minutos. Durante un mes decido probar una nueva ruta B y observo que demoro 23 minutos. ¿Es realmente la ruta B más rápida que la ruta A? ¿O por el contrario esa diferencia de 2 minutos se debe a la casualidad, por ejemplo, porque durante ese período el tráfico ha sido especialmente fluido?

Si la diferencia no se debe al azar, diremos que es una diferencia estadísticamente significativa.

Situaciones en las que necesitamos estar seguros de que las diferencias que observamos no se explican por puro azar son numerosas. Es la base del método científico. Por ejemplo, pensemos en la investigación médica. Tenemos un nuevo fármaco y queremos verificar si produce el efecto deseado. Para ello, administramos a una muestra de personas el fármaco y comparamos los resultados con una muestra de personas que no han sido tratadas, o mejor aún, que han sido tratadas con un tratamiento placebo. Cuando obtengamos los resultados, necesitamos estar seguros de que el efecto curativo es real. Este tipo de pruebas son las que los productos homeopáticos no superan y la razón por la que la comunidad médica no los acepta como eficaces.

Con la llegada de Internet, esta metodología de trabajo se ha puesto más de moda que nunca. Pensemos en los tests A/B que se utilizan tan frecuentemente en el desarrollo de páginas web. Por ejemplo, tenemos una web de comercio electrónico en la que el 5% de los visitantes acaban comprando un producto. Queremos testar si incrementar el tamaño de las imágenes de los productos mejora las ventas. Hacer un test A/B consistiría en poner en funcionamiento una nueva versión de la web, mostrar aleatoriamente a los usuarios una de las dos versiones y medir qué éxito de ventas tiene cada una. Si la nueva web tiene un éxito de ventas del 5,5%, ¿podemos estar seguros de que esa diferencia de 0,5% se debe a las imágenes más grandes?

Para responder a estas cuestiones, la estadística nos va a ser de utilidad. Necesitamos hacer un test de hipótesis. Veamos como funciona.

Test de hipótesis

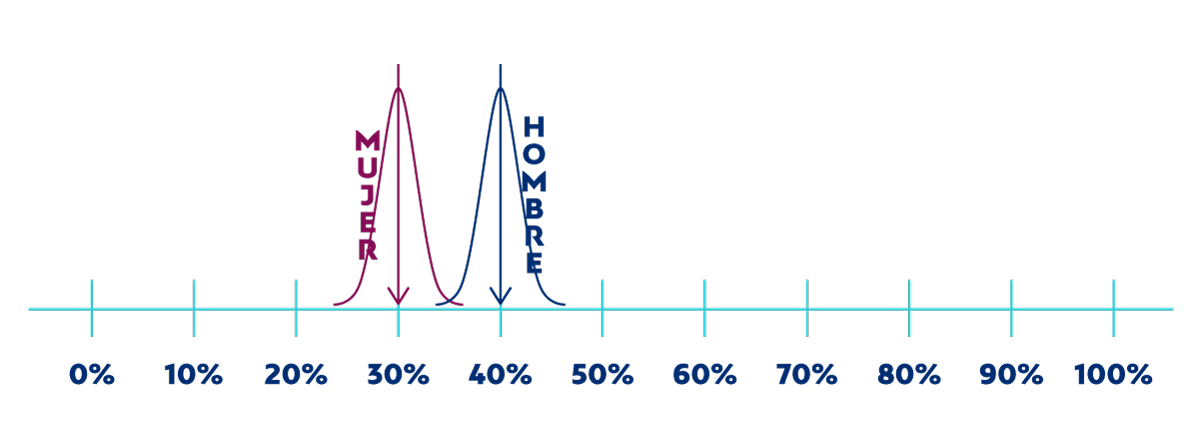
Para empezar, vamos a dar una idea intuitiva lo que estamos haciendo. Supongamos que hacemos una encuesta a 100 hombres y a 100 mujeres preguntando si practican deporte. Analizando las respuestas, observamos que el 40% de los hombres afirman practicar deporte frente al 30% de las mujeres. Podríamos representar este dato con el siguiente gráfico:

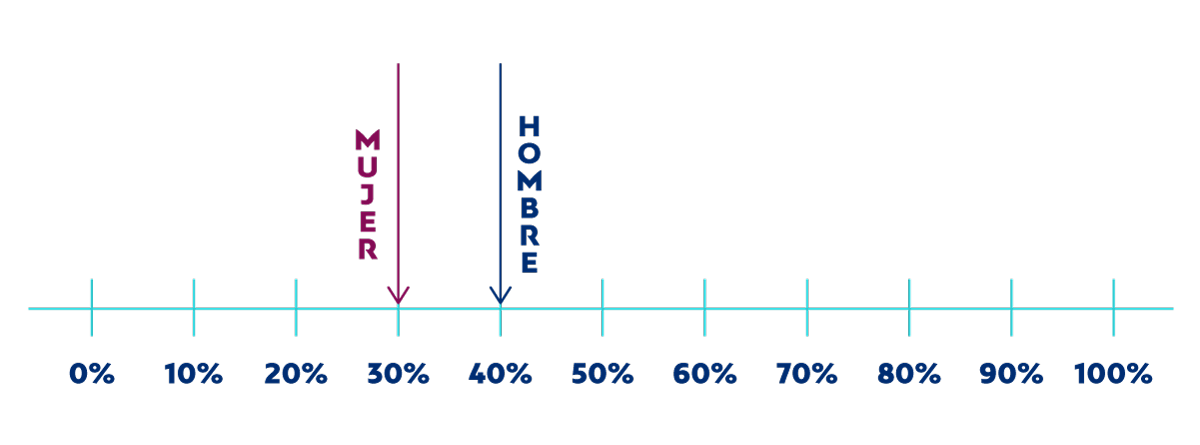
Pero vimos en un post anterior que al calcular una estadística usando una muestra de gente (en lugar del universo completo), nuestro dato no va a ser preciso sino que estará dentro de un margen de error. Este margen es mayor cuanto más pequeña es la muestra que empleamos. Por ello, sería más correcto representar el resultado de esta encuesta con un gráfico como el que sigue a continuación: 

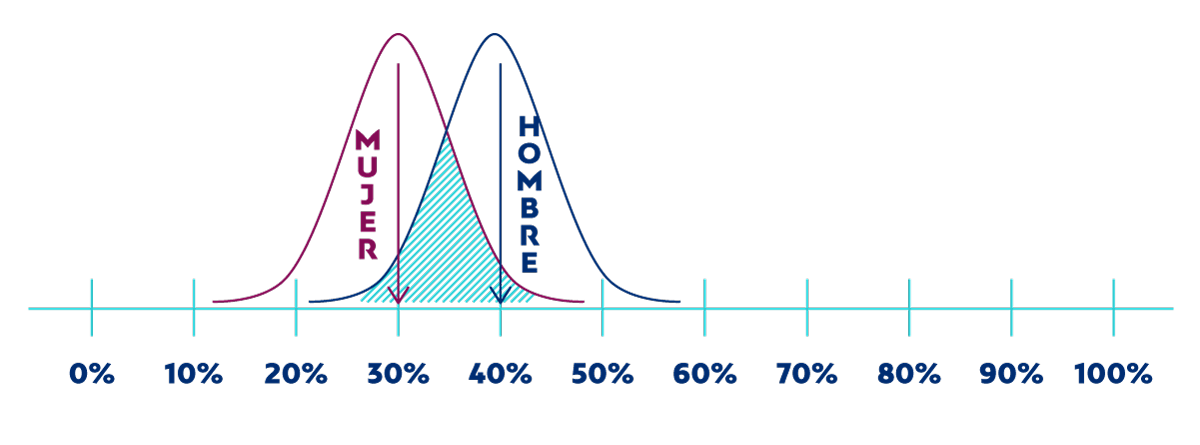
 En este gráfico, hemos representado la incertidumbre que tenemos acerca de los porcentajes de hombres y mujeres que practican deporte. Cuando empleamos esta mirada, vemos que el margen de error de ambos datos (hombres y mujeres) se solapa de forma considerable.

En el ejemplo que hemos representado, el gráfico nos indica que es relativamente fácil que esa diferencia observada entre hombres y mujeres no sea real, sino que sea simplemente un efecto del error muestral que se tiene por trabajar con una muestra reducida. La porción gris representa ese riesgo: es la probabilidad de que la diferencia se deba al error. Tendríamos, por lo tanto, una diferencia no significativa.

¿Cómo podríamos estar seguros de que la diferencia sí es realmente significativa?

Idealmente, si la diferencia entre los datos de hombres y mujeres fuese mayor, de forma que el margen de error de cada dato se solapase mucho menos, como se representa a continuación:

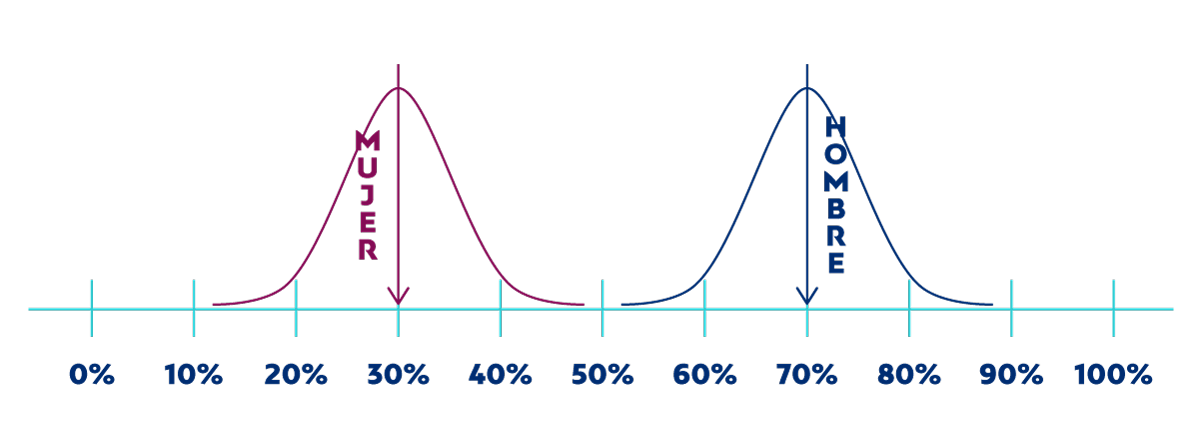
 Obviamente, eso no depende de nosotros. Por lo que, si quisiéramos tener mayor seguridad sobre si la diferencia es significativa, tendríamos que trabajar con tamaños de muestra superiores. O dicho de otra manera, si la diferencia esperada va a ser pequeña, necesitamos trabajar con una muestra mayor, lo que genera un margen de error más pequeño y permitirá detectar diferencias significativas menores, tal y como se muestra en la gráfica siguiente.

¿Y esto se puede medir objetivamente?

Sí, para eso se suele realizar un test de hipótesis, que es una prueba objetiva sobre la causa de las diferencias.

En primer lugar, definimos las siguientes cantidades:

• Nh = tamaño de la muestra de hombres.

• Nm = tamaño de la muestra de mujeres.

• Xh= números de hombres que practican deporte.

• Xm= números de mujeres que practican deporte.

A partir de estas cantidades, calcularemos la proporción global de personas que practican deporte, sean hombres o mujeres. Sería:

• P = (Xh+Xm)/(Nh+Nm)

También podemos calcular la proporción de deportistas entre hombres y entre mujeres, que son los datos que han resultado diferentes y queremos verificar.

• Ph = Xh/Nh

• Pm = Xm/Nm

A continuación, planteamos las dos hipótesis posibles:

• H0 (hipótesis nula) = no hay diferencias entre las muestras, la diferencia observada se debe al azar.

• H1 (hipótesis alternativa) = la diferencia es estadísticamente significativa, ambas muestras realmente son diferentes en relación a la variable estudiada.

Para poder aceptar la hipótesis alternativa, necesitamos que la diferencia entre las dos proporciones medidas (Ph y Pm) diste lo suficiente como para tener un % de confianza suficientemente alto de que esa diferencia no se deba al error muestral, suponiendo que dicho error sigue una distribución gaussiana o normal. Para ello, emplearemos una prueba-Z, que es la que se utiliza para comparar proporciones entre dos muestras distintas. Tendremos que calcular lo siguiente:

y comprobar que la Z resultante no supera una cantidad que viene dada por el nivel de confianza que deseamos. Es muy habitual trabajar con un intervalo de confianza del 95%, al cual corresponde un valor de Z=1,96. Por lo tanto:

• Si Zprueba<1,96, aceptaremos que NO hay diferencias significativas entre hombres y mujeres, con un nivel de confianza del 95%.

• En caso contrario, SÍ aceptaremos que la diferencia observada entre hombres y mujeres es significativa con un nivel de confianza del 95%.

Volviendo al ejemplo...

Podemos hacer estos cálculos en nuestro ejemplo inicial. Recordemos: 100 hombres y 100 mujeres, 40 hombres deportistas y 30 mujeres deportistas. Tendríamos:

• Nh = 100.

• Nm = 100.

• Xh= 40.

• Xm= 30.

Estos datos resultan en Z=1,48, que al ser inferior a 1,96 no nos permitiría afirmar que la diferencia es significativa. Si por el contrario este resultado se hubiese obtenido con una muestra de 200 hombres y 200 mujeres, la Z resultante sería de 2,10, lo que nos permitiría aceptar la hipótesis.

Algunas consideraciones finales

Es muy importante tener en cuenta con qué tamaño de muestra trabajamos. En ocasiones, con muestras extremadamente pequeñas, se observan diferencias muy grandes, que aún así, no tienen significancia estadística. Eso no significa que esa diferencia no sea real, simplemente quiere decir que con los datos que tenemos no podemos tener una garantía suficiente de que sea real.

En sentido contrario, con muestras extremadamente grandes, podemos encontrar diferencias significativas pequeñas, que en la práctica no van a resultar muy informativas.

Por último, tenemos en nuestra página web dos calculadoras de diferencias significativas, para medias y para proporciones, con el fin de ayudarte a hacer estos cálculos. Las encontrarás aquí.