En una época en la que prácticamente todo es cuestionado, la ciencia permanece como el único valor seguro, el "centro de gravedad permanente" que cantaba Franco Battiato. Ya no nos creemos nada que no vaya con la coletilla de "estudios científicos demuestran que...".
Las empresas y organizaciones lo han entendido perfectamente. Por eso entran en el terreno científico para demostrar la bondad de su productos, de sus propuestas. Y la estadística es un elemento fundamental de la ciencia. Probablemente la herramienta que explica el tremendo impulso que hemos observado en el conocimiento y la tecnología en los últimos 100 años.
Pero la estadística es un arma de doble filo, fácilmente manipulable cuando la audiencia a la que nos dirigimos no maneja el lenguaje y los fundamentos que la sostienen. ¿Cómo es posible que salgan a la luz estudios que demuestran que la sal es mala al mismo tiempo que otros demuestran que la sal es buena? ¿Cómo pueden ser las proteínas buenas y malas al mismo tiempo? ¿Y la grasa dañina y beneficiosa a la vez?
Cómo hacer creer a millones de personas que el chocolate adelgaza
Este extraordinario post publicado por John Bohannon nos explica cómo es posible usar la estadística para hacer creer a la población cualquier cosa.
John, en colaboración con un periodista, Peter Onneken, decidieron mostrar al mundo cómo funcionan los falsos estudios científicos. Para ello, costearon un estudio sobre una reducida muestra de individuos, divididos en 3 grupos:
- Grupo 1 - Individuos a los que se les asignó una dieta baja en carbohidratos durante 21 días consecutivos.
- Grupo 2 - Individuos que siguieron la dieta del grupo 1 pero que además debían ingerir una onza y media de chocolate diariamente.
- Grupo 3 - Grupo de control, personas que siguieron su dieta habitual.
Tras estudiar los datos desde diferentes puntos de vista, John y Peter encontraron que los grupos 1 y 2, los de la dieta, habían perdido en torno a 700 gramos de peso, mientras que el grupo 3, el de control, no. Pero los individuos del grupo 2 habían perdido el peso un 10% más rápido que el grupo 1, una diferencia estadísticamente significativa. Además, sus niveles de colesterol eran mejores así como algún otro indicador relacionado con su estado de salud.
¡Bingo! Ya tenían lo que andaban buscando: una dato estadísticamente válido que indicara el beneficio de tomar chocolate para perder peso. Seguramente te estarás preguntando qué tiene de malo este estudio. Si el dato ha resultado significativo, ¿acaso no es cierta la conclusión del estudio? ¿No es así como funciona la ciencia?
La trampa está en un pequeño secreto a voces acerca del uso de la estadística en estudios científicos: si mides un gran número de cosas sobre un grupo pequeño de individuos, tienes casi garantizado encontrar algo "estadísticamente significativo". John midió en su estudio 18 parámetros diferentes - peso, colesterol, nivel de sodio... - sobre tan sólo...¡15 personas!. El estudio estaba diseñado para generar "falsos positivos".
En su artículo, John hace una metáfora que explica bien esta forma de diseñar un estudio. Es similar a comprar boletos de lotería. Cada boleto de lotería tiene pocas posibilidades de resultar premiado, así como cada parámetro de salud tenía pocas posibilidades de mostrar una diferencia significativa. Pero al incluir 18 parámetros en un estudio, tus posibilidades de resultar premiado crecen. John no sabía si iba a encontrar un beneficio del chocolate en relación a la pérdida de peso o la tensión sanguínea, pero sabía que tenía muchas posibilidades de dar con "algo significativo".
Hablaremos más sobre este tema en futuros posts, pero piensa qué significa exactamente "estadísticamente significativo". Está relacionado con algo que se conoce como el p-value. Cuando obtenemos un resultado de un estudio, siempre reportamos el p-value, que es la probabilidad de que ese resultado se haya producido por simple azar. Habitualmente se considera que el resultado es significativo y, por tanto, no se debe al azar sino a una causa sustancial, si el p-value está por debajo del 5%.
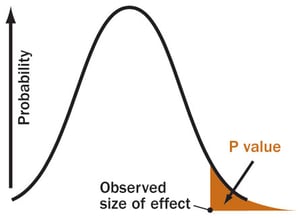
Cuando mostramos un p-value por debajo del 5%, logramos un efecto automático en nuestra audiencia: la credibilidad del método científico. Sin embargo, cuando hacemos un estudio con el diseño empleado por John (poca muestra y muchos parámetros medidos), las probabilidades de dar con alguna diferencia entre los grupos estudiados con un p-value por debajo del 5% aumentan según la fórmula siguiente.
P(winning) = 1 - (1 - p)n
Con n=18, la probabilidad de éxito es del 60%. Este fenómeno se conoce como p-hacking. Muchos científicos honestos hacen p-hacking de forma inconsciente. En ocasiones, quieren probar una hipótesis, obtienen resultados negativos y repiten el experimento hasta que "funciona". Es el mismo problema: están comprando boletos de lotería hasta que ganan.
¿Cómo logra difusión un estudio tan poco riguroso?
La respuesta es: gracias al poco rigor científico de muchas publicaciones, combinado con las ganas de lanzar en medios una noticia sensacionalista. Esta fue la conclusió de John y Peter: varias de las revistas que contactaron, supuestamente científicas, publicaron los resultados sin hacer peer-review (revisión de otro científico). En cuanto el estudio se publicó, los medios generalistas se lanzaron a publicarlo: en el momento en que apareció en el Bild ("Los que comen chocolate siguen delgados"), otros medios siguieron su camino, como el Daily Star, el Irish Examiner, Cosmopolitan’s de Alemania, el Times of India, las versiones alemana e india del Huffington Post, incluso la television de Texas y un show televisivo australiano.
Un fenómeno curioso observado por John es la forma en que se presentó el estudio en muchos medios: normalmente acompañado de imágenes prácticamente pornográficas de personas comiendo chocolate de forma lasciva. Por si acaso alguien no estaba interesado en el resultado, supongo.

Pocos medios contactaron con John para conocer los detalles del estudio. Los pocos que lo hicieron, no hicieron la pregunta clave: ¿cuánta gente participó en el estudio? Si alguien hubiese sabido que se trataba de 15 personas, seguramente el impacto habría sido muy diferente.
John y Peter demostraron así lo simple que es lograr engañar a la opinión pública de forma interesada. Ya sabes ahora cómo es posible que aparezcan estudios en los que pueda demostrarse cualquier cosa, desde que comer pescado nos hace más pacíficos a que leer las etiquetas de los alimentos te mantiene delgado.
Es por ello que recomiendo que, antes de dar credibilidad a cualquier cosa que veas publicada, mires la ficha técnica del estudio (número de personas y método empleado en el estudio), la reputación de quién publica, quién ha pagado el estudio y, muy importante, que busques qué hipótesis soporta los resultados observados. Recuerda que correlación no es causalidad y muchos estudios estadísticamente bien planteados también confunden ambos fenómenos.






