Uma das seções do nosso site mais visitadas é a calculadora de amostras: uma aplicação online que te indica quantas pessoas você deveria entrevistar para estimar um dado de uma população sem superar um nível máximo de erro.
Frequentemente recebemos consultas sobre o que faz essa calculadora: que fórmulas utiliza, o que significam termos como margem de erro ou nível de confiança. Hoje te explicamos como funciona exatamente e que tamanho amostral você precisa para abordar uma pesquisa.
O problema
Imagine que você quer saber qual porcentagem da população brasileira entre 15 e 65 anos fuma. Ou quantos minutos por dia assistem à televisão. Obviamente, o ideal seria perguntar a todos os membros da população (136 milhões), mas isso é extremamente caro. Por isso, normalmente optamos por entrevistar uma parte da população, o que é conhecido como uma amostra. Como uma amostra não contém todos os indivíduos, inevitavelmente vamos cometer algum erro em nossas estimativas. Quanto menor for a amostra, esse erro poderá ser potencialmente maior.
Mas é possível garantir que o erro de estimativa não supere certos limites? Sim, é possível e vamos ver como.
Um pouco de teoria: o teorema central do limite
Para começar, simplifiquemos um pouco o problema. A população brasileira entre 15 e 65 anos é muito grande, podemos considerá-la uma população infinita. Essa suposição é muito prática: permite aceitar que toda vez que seleciono um indivíduo para minha amostra, sua probabilidade de ter a característica que quero medir (por exemplo, fumar) é constante, independentemente dos indivíduos que já tenha selecionado anteriormente. Veremos depois o que fazer se não posso aceitar a suposição de população infinita.
Se aceitarmos essa simplificação, podemos utilizar o teorema central do limite. Este teorema diz que se obtivermos múltiplas amostras de \( n \) indivíduos de uma população infinita, a média dessas amostras tende a uma distribuição Normal centrada na média da população. E diz algo mais: essa distribuição Normal tem um desvio padrão igual ao desvio da população de origem dividido por \( \sqrt{n} \).
Vejamos o que isso significa na prática. Voltemos à população brasileira, aos 136 milhões. Imagine por um momento que pudéssemos observar todos os indivíduos e medir quanto tempo assistem à televisão. Uns assistirão pouco, outros muito… mas com todos os indivíduos poderíamos calcular uma média exata (suponhamos 400 minutos). Também poderíamos calcular o desvio padrão da população, uma medida da dispersão dos indivíduos em relação à média (por exemplo, 100 minutos).
Agora suponha que obtemos uma amostra aleatória simples de \( n \) pessoas e observamos quanto assistem à TV. A média nesta primeira amostra deve ser similar à média da população (400), mas seguramente não será exata. Poderia ser 380, por exemplo. A seguir, obtemos um segundo tamanho amostral e resulta em uma média de 415. E uma terceira, e uma quarta… E assim por diante. A sequência poderia ser algo assim.
Amostra 1 -> Média observada 380
Amostra 2 -> Média observada 415
Amostra 3 -> Média observada 405
Amostra 4 -> Média observada 394
...
O que nos diz o teorema central do limite é que essas médias que observamos nas amostras de \( n \) indivíduos formam, por sua vez, uma distribuição de probabilidade Normal. A média dessa distribuição de médias coincide com a média da população original, que chamaremos de \( \mu \) . E o desvio dessa distribuição de médias é igual ao desvio original (que chamaremos de \( \sigma \) ) dividido por \( \sqrt{n} \) . Ou seja, \( \sigma / \sqrt{n} \) . E essa é a razão pela qual quanto maior o tamanho de uma amostra, mais precisa é a estimativa: a distribuição de médias está mais concentrada em torno da média da população e, portanto, é mais provável que a média da amostra se aproxime da média da população.
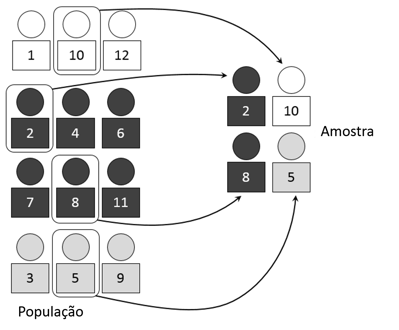
O esquema a seguir pode te ajudar a entender o teorema central do limite.
O teorema central do limite funciona mesmo que a população original não se distribua de forma Normal. Ele se cumpre para qualquer distribuição. No final, as médias das amostras se distribuem de forma Normal. E isso é o que nos permite medir e limitar o erro de nossas estimativas.
Pode te interessar: Questionário e pesquisa: como se diferenciam?, O que é uma pesquisa por amostragem?, Amostragem, o que é e por que funciona, Tipos de itens em pesquisas online.
Margem de erro e nível de confiança
Já sabemos o que podemos esperar se obtivermos muitas amostras de nossa população. Mas, na prática, temos apenas uma amostra de tamanho \( n \) . No entanto, saber que esta amostra faz parte de uma distribuição de médias nos ajuda.
Uma distribuição Normal tende a estar concentrada em torno da média. E sabemos em que medida. Por exemplo, sabemos que em 90% dos casos, a média da amostra estará em um intervalo \( \mu \pm 1.645 \cdot \sigma / \sqrt{n} \). Ou que em 95% dos casos, a média estará em um intervalo \( \mu \pm 1.96 \cdot \sigma / \sqrt{n} \).
A relação entre "os 90% dos casos" (conhecido como nível de confiança) e o valor "1.645" (conhecido como Z-score) é uma propriedade da distribuição Normal. Podemos definir outros níveis de confiança. Habitualmente, são usados níveis de confiança (NC) de 80%, 90%, 95% e 99%, aos quais correspondem os Z-scores 1.282, 1.645, 1.960 e 2.576.
|
Nível de confiança (NC) |
Z-score
|
| 80% | 1.282 |
| 90% | 1.645 |
| 95% | 1.960 |
| 97% | 2.170 |
| 99% | 2.576 |
Portanto, de forma geral, podemos dizer que a média que medimos na amostra (\( m \)) cumpre o seguinte:
$$ P\left( \mu - Z_{NC} \cdot \frac{\sigma}{\sqrt{n}} < m < \mu + Z_{NC} \cdot \frac{\sigma}{\sqrt{n}} \right) = NC $$
A expressão anterior se lê assim: a probabilidade de que a média \( m \) observada na amostra esteja entre o intervalo definido pela média da população \( \mu \) menos a margem de erro \( Z_{NC} \cdot \sigma / \sqrt{n} \) e a média da população mais a margem de erro \( Z_{NC} \cdot \sigma / \sqrt{n} \) , é \( NC \) .
Como o que queremos estimar é justamente a média da população \( \mu \), podemos transformar a expressão anterior da seguinte forma, trocando a ordem dos elementos da desigualdade:
$$ P\left( m - Z_{NC} \cdot \frac{\sigma}{\sqrt{n}} < \mu < m + Z_{NC} \cdot \frac{\sigma}{\sqrt{n}} \right) = NC $$
Para entender melhor essa expressão, retomemos o exemplo anterior sobre a população brasileira. Suponha que obtemos uma amostra de \( n=500 \) pessoas, calculamos a média de minutos de TV assistidos por essas 500 pessoas e resulta 415. E suponha por enquanto que sabemos que o desvio padrão na população não supera os 100 minutos. Poderíamos dizer:
$$ P\left( 415 - 1.645 \cdot \frac{100}{\sqrt{500}} < \mu < 415 + 1.645 \cdot \frac{100}{\sqrt{500}} \right) = NC $$
$$ P\left( 415 - 7.4 < \mu < 415 + 7.4 \right) $$
$$ P\left( 407.6 < \mu < 422.4 \right) $$
Graças ao teorema central do limite, podemos dizer que em 90% dos casos, a média de consumo de TV da população brasileira está entre 407.6 e 422.4 minutos. Em vez de dar uma estimativa pontual (415), estamos dando uma estimativa com uma margem de erro (±7.4) e o nível de confiança que temos de que a realidade esteja dentro da margem de erro (90%).
E como isso me ajuda a decidir o tamanho da amostra?
Muito fácil, você só precisa decidir de antemão qual é o erro máximo que está disposto a aceitar ( \( e \) ) e o nível de confiança que deseja ter de que esse erro não será superado ( \( NC \) ).
Sabendo que o erro máximo é:
$$ e \leq Z_{NC} \cdot \frac{\sigma}{\sqrt{n}} $$
basta inverter essa expressão:
$$ n \geq \frac{Z_{NC}^2 \cdot \sigma^2}{e^2} $$
Voltando ao nosso exemplo. Imagine que ainda não fizemos a pesquisa, mas queremos ter um nível de confiança de 90% de que a média que observamos na amostra não se desvie da realidade em mais de ±5 minutos. A amostra que precisamos será de:
$$ n \geq \frac{1.645^2 \cdot 100^2}{5^2} = 1,082.4 \approx 1,083 $$
Arredondamos para cima (1,082.4 → 1,083) porque queremos garantir que não superamos o erro de 5 minutos, mas é um detalhe sem muita importância. Observe que a amostra resultante é maior do que a anterior de 500 indivíduos, porque o erro máximo que pedimos (5) é menor do que o que tínhamos antes (7.4).
E se o que eu quero estimar é uma proporção?
Suponha que, em vez de estimar uma média (minutos de TV), quero estimar uma proporção (percentual de fumantes). Nesse caso, o problema é mais simples, podemos simplificar as fórmulas anteriores de forma muito conveniente.
Chamemos \( p \) ao percentual de fumantes no total da população brasileira. Nesse caso, a população se distribui seguindo uma distribuição de Bernoulli: uma proporção \( p \) da população fuma (fumar=1) e uma proporção \( 1-p \) não fuma (fumar=0). Essa distribuição é extremamente simples e tem um desvio padrão \( \sigma = \sqrt{p(1 - p)} \). Portanto, o tamanho da amostra que garante um erro máximo \( e \) é:
$$ n \geq Z_{NC}^2 \cdot \frac{p \cdot (1 - p)}{e^2} $$
Podemos simplificar um pouco mais essa expressão. Antes de fazer a pesquisa, não sabemos qual proporção de fumantes vamos encontrar (para isso fazemos a pesquisa). Mas podemos nos colocar no pior caso. Observe que a quantidade \( p(1 - p) \) resulta 0 tanto se \( p=0 \) como se \( p=1 \) . Ou seja, se todo mundo fuma ou não fuma, a amostra que precisamos é praticamente nula. O pior caso ocorre quando a população é o mais diversa possível ( \( p=0.5 \) ), ou seja, quando metade das pessoas fuma.
Se usar esse cenário pessimista, resulta:
$$ n \geq \frac{Z_{NC}^2}{4e^2} $$
Ao contrário do caso em que estimávamos minutos de TV vistos, não precisamos fazer nenhuma hipótese sobre o desvio padrão da população de origem, porque podemos usar o pior caso: a máxima variação possível em uma proporção.
Como se usa essa fórmula? Suponha que queremos fazer uma pesquisa entre brasileiros para estimar qual percentual da população fuma e estamos dispostos a aceitar um erro máximo de 5% com um nível de confiança de 90%. Resulta:
$$ n \geq 1.645^2 \cdot \frac{1}{4 \times 0.05^2} \approx 271 $$
Precisamos entrevistar apenas 271 pessoas. Importante: o erro é definido em termos absolutos. Ou seja, se observamos um 40% de fumantes, teremos 90% de confiança de que a proporção real na população está entre 40%-5% e 40%+5% (não entre 40%×0.95 e 40%×1.05).
E se a população não for infinita?
Costuma-se aceitar que uma população com mais de 100.000 indivíduos é infinita (alguns autores consideram 50.000 como o mínimo exigível). Em geral, na pesquisa de mercados, as populações objeto de estudo costumam cumprir esse requisito. Mas em determinados casos podemos ter populações pequenas. Por exemplo, uma pesquisa com funcionários de uma empresa.
Nesses casos, as fórmulas que vimos devem ser modificadas um pouco. Vamos ajudá-lo a entender o porquê. Imagine um caso muito extremo em que há apenas 10 pessoas na população, metade fumantes e a outra metade não fumantes. E você quer uma amostra de 2 pessoas.
Inicialmente, você tem 50% de probabilidade de que o primeiro indivíduo de sua amostra seja fumante. Você seleciona um indivíduo e fuma. A probabilidade de que o segundo indivíduo seja fumante já não é 50%, porque restam apenas 4 fumantes entre os 9 indivíduos não selecionados. Agora a probabilidade de que você selecione um fumante é 4/9=44%. A probabilidade de que fumem os indivíduos a serem selecionados depende dos já selecionados.
Essa dificuldade pode ser ignorada quando a população é de centenas de milhares de indivíduos (quando \( N \) é muito grande), porque quando a população é grande, o efeito de retirar um ou dois indivíduos não altera as proporções. Mas quando a população é pequena, o tamanho da amostra deve ser ajustado de acordo com a população total. Portanto, a fórmula para calcular o tamanho da amostra de uma população finita é:
$$ n_{ajustada} = \frac{n_{infinita}}{1 + \frac{n_{infinita}-1}{N}} $$
Essa fórmula ajusta o tamanho da amostra para garantir que os elementos selecionados tenham proporções representativas. Vamos ver como se aplica.
Imagine que deseja realizar uma pesquisa em uma população de 50 pessoas para avaliar a porcentagem de fumantes, onde calculou previamente que precisava entrevistar 50 pessoas. Nesse caso, o que você deve fazer é:
$$ n_{ajustada} = \frac{50}{1 + \frac{50-1}{50}} = \frac{50}{1 + 0.98} = 25.1 \approx 25 $$
O tamanho da amostra ajustada seria de 25 indivíduos. Como você vê, isso não se ajusta ao que observou antes, porque a porcentagem da população influencia o tamanho da amostra necessário. Esse ajuste é feito para garantir que a amostra seja representativa da população total.
Mas e se o orçamento for limitado?
Os cálculos anteriores se baseiam na premissa de que há um número suficiente de pesquisas. No entanto, na prática, o orçamento pode ser um fator limitante. Sugiro que você faça uma análise de custo-benefício para garantir que o tamanho da amostra seja economicamente viável.
A relação entre a população, o tamanho da amostra, o erro e o custo deve ser avaliada cuidadosamente para garantir que as metas do estudo sejam cumpridas. Em alguns casos, pode ser necessário ajustar suas expectativas de precisão ou o nível de confiança à medida que determina seu tamanho de amostra.
